Here are some suggestions of how we could define a tangent to a curve at a point.
Which, if any, of these proposed definitions works for a circle?
For each one, can you find or sketch an example to show that the proposed definition does not work for all curves?
All four of the proposed definitions work for circles. Things only stop working when we allow other types of curves.
“A tangent is a straight line which only meets the curve at that one point.”
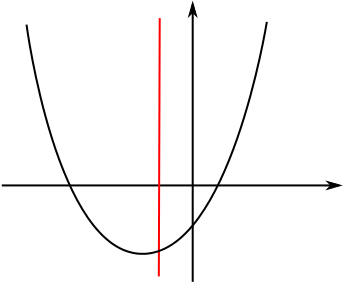
Here’s a case where it meets at more than one point:
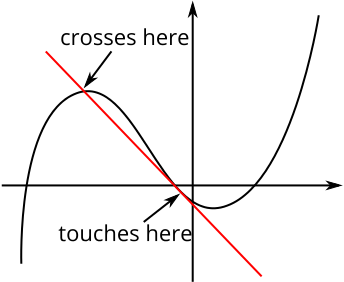
And here’s a straight line which only meets the curve at one point, but is clearly not what we would want to call a tangent:
“A tangent is a straight line which touches the curve at that point only.”
Here’s a case where a tangent touches the curve at more than one point:
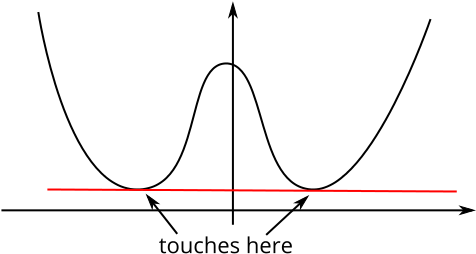
“A tangent is a straight line which meets the curve at that point, but the curve is all on one side of the line.”
The first example for statement 1 above shows that this doesn’t work, either.
“A tangent is a straight line which meets the curve at that point, but near that point, the curve is all on one side of the line.”
This is better than statement 3, but the graph of \(y=x^3\) shows that this doesn’t quite work either. (This same example also shows that statement 3 does not always work.) A rough sketch looks like this; the tangent is the \(x\)-axis:
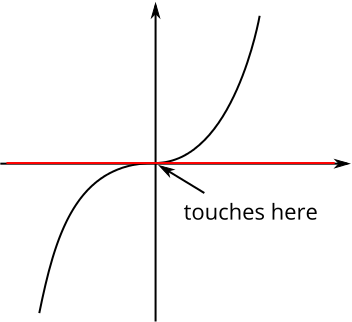
Can you come up with a better definition?
As we saw in Zooming in, when we “zoom in” to a point on a curve, it often looks like a straight line. If so, then we can draw that straight line. If we then zoom out again, we will discover that we have drawn the tangent to the curve at that point. This is what a tangent is.
Here is an example for the function \(y=x^2\) at \(x=1\):
We start with the graph of \(y=x^2\):
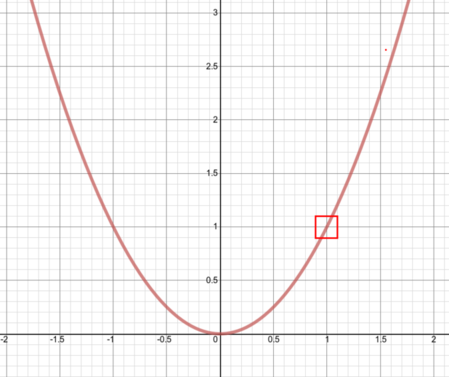
We zoom in to \((1,1)\) (indicated by the red box):
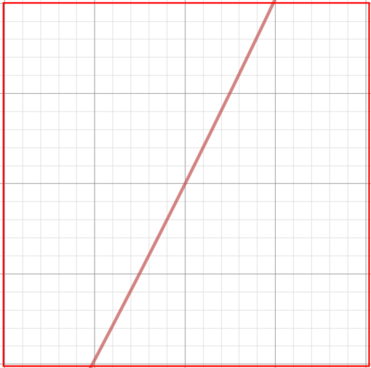
It looks just like a straight line! So we draw that line on the graph as well (\(y=2x-1\)), here shown in blue:
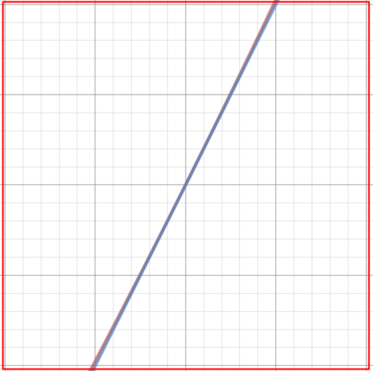
We now zoom back out:
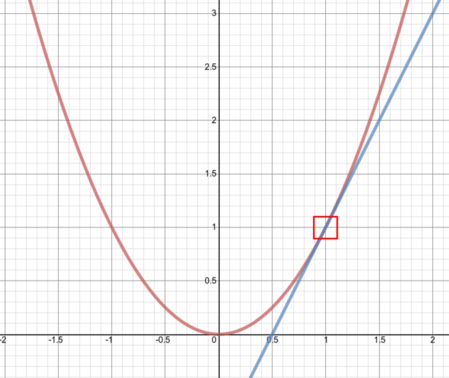
You can explore this idea yourself using the interactive graph or graphing software such as Desmos.
This problem tells us that a tangent is a local property of a graph: the tangent at a point is dependent upon the behaviour of the graph very near that point. What goes on elsewhere on the graph is of no interest when finding the tangent.
The gradient of a curve at a point is similarly a local property.
Can you find a graph which does not look like a straight line when you zoom in? (This may only be at one particular point.)
Would the graph have a tangent at that point?

