Night trains run non-stop between King’s Cross and Edinburgh, a distance of \(392\) miles, as follows:
Edinburgh depart 10.00 p.m. King’s Cross depart 10.20 p.m.
King’s Cross arrive 6.10 a.m. Edinburgh arrive 5.48 a.m.
- Calculate the average speed of each train in m.p.h.
The train from Edinburgh to King’s Cross takes \(8\) hours and \(10\) minutes for the \(392\) miles. Since \(1\) minute corresponds to \(\dfrac{1}{60}\) hours, the whole journey takes \(8+\dfrac{1}{6} = \dfrac{49}{6}\) hours. Therefore, the average speed of the first train is \(\dfrac{392}{\left(\dfrac{49}{6}\right)} = 48\) m.p.h.
The train starting at King’s Cross needs \(7\) hours and \(28\) minutes, i.e. \(7 + \dfrac{28}{60} = \dfrac{112}{15}\) hours, to reach Edinburgh. That gives an average speed of \(\dfrac{392}{\left(\dfrac{112}{15}\right)} = 52.5\) m.p.h. for the second train.
- If each train were to maintain a constant speed, find at what time the two trains would meet and at what distance from Edinburgh.
(A graphical method is recommended for this part of the question.)
Approach 1
Consider the sketch picture, where the graph representing the train starting in Edinburgh is \(y = 48x\).
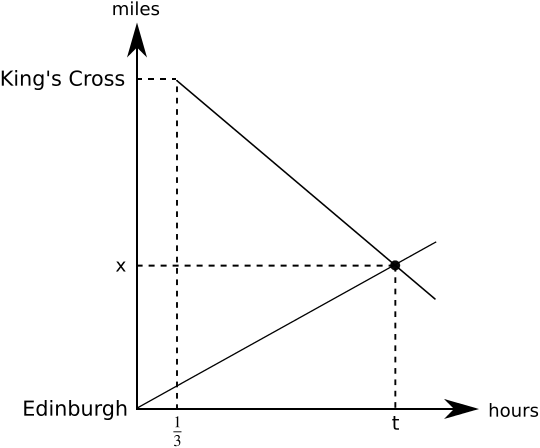
As the graph describing the train starting at King’s Cross has slope \(-52.5\), it can be described by \(y = -52.5x + b\), where \(b\) is the \(y\)-intercept.
To work out \(b\), we use that the graph passes through the point \(\left(\dfrac{1}{3}, 392\right)\). We have \(392 = -52.5\times \dfrac{1}{3} + b\) and hence \(b = 409.5\).
The meeting point for the trains is given by \(-52.5x + 409.5 = 48x\), or \(409.5 = 100.5x.\)
This yields \(x = \dfrac{273}{67}\), or \(4\) hours and \(4\) minutes, and therefore the trains meet at \(2.04\) a.m.
The trains meet \(48 \times \dfrac{273}{67} \approx 195.6\) miles from Edinburgh.
Approach 2
The train starting at Edinburgh leaves \(20\) minutes (i.e. \(\dfrac{1}{3}\) hours) earlier than the train starting at King’s cross.
Since the earlier train has an average speed of \(48\) m.p.h. it has already travelled \(\dfrac{1}{3} \times 48 = 16\) miles when the second train sets off.
Suppose that the first \(20\) minutes are already over. Let us write \(t\) for the hours it now takes the two trains to meet.
That means that the train starting at Edinburgh travels another \(48t\) miles, and the train starting in King’s Cross travels \(52.5t\).

As the total distnce between Edinburgh and King’s cross is \(392\) miles, we get the equation \(392 = 16 + 48t + 52.5t\), which gives \(t = \dfrac{752}{201}\), or approximately \(3\) hours and \(42\) minutes.
Since the train from Edinburgh started \(20\) minutes before the other, the trains meet \(4\) hours and \(4\) minutes after the first train left Edinburgh, which is at \(2.04\) a.m.
The train starting in Edinburgh has an average speed of \(48\) m.p.h. and therefore travels \(\dfrac{752}{201} \times 48 + 16 \approx 195.6\) miles, which is the distance from Edinburgh at which the two trains meet.

