When the trapezium rule is used to estimate the integral
\[\int_0^1 \! 2^x \, \mathrm{d}x\]
by dividing the interval \(0 \le x \le 1\) into \(N\) subintervals the answer achieved is
\(\dfrac{1}{2N} \left(1+\dfrac{1}{2^{1/N}+1} \right)\),
\(\dfrac{1}{2N} \left(1+\dfrac{2}{2^{1/N}-1} \right)\),
\(\dfrac{1}{N} \left(1-\dfrac{1}{2^{1/N}-1} \right)\),
\(\dfrac{1}{2N} \left(\dfrac{5}{2^{1/N}+1} -1\right)\).
The trapezium rule says this:
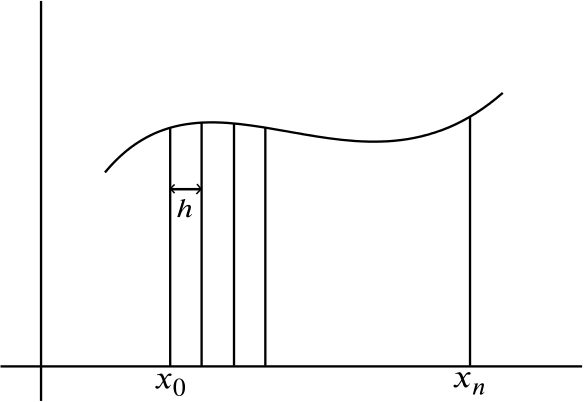
The area under the curve \(f(x)\) between the points \(x_0\) and \(x_n\), with this interval divided into \(n\) smaller intervals of width \(h = \dfrac{(x_n - x_0)}{n}\) is given by
\[\displaystyle\int_{x_0}^{x_n} \! f(x) \, \mathrm{d}x \approx \dfrac{1}{2} h \left[ (y_0 + y_n) + 2(y_1 + y_2 + \dotsb + y_{n-1} ) \right],\]
where \(y_i = f(x_i)\).
So dividing the interval \(0 \le x \le 1\) into \(N\) subintervals for our problem gives \(h=\dfrac{1}{N}\), and the trapezium rule gives
\[\begin{align*} \displaystyle\int_0^1 \! 2^x \, \mathrm{d}x \hspace{2mm} & \approx \dfrac{1}{2} \dfrac{1}{N} \left[ (2^0 + 2^1) + 2(2^{\frac{1}{N}}+2^{\frac{2}{N}}+ ... + 2^{\frac{N-1}{N}}) \right] \\ \end{align*}\]We have what looks like a series inside the brackets. Do we know any ways of simplifying series?
\[2^{\frac{1}{N}}+2^{\frac{2}{N}}+ ... + 2^{\frac{N-1}{N}}\]
is a geometric series with a first term of \(2^{\frac{1}{N}}\), a common ratio of \(2^{\frac{1}{N}}\), and \(N-1\) terms so we can write it as,
\[\dfrac{2^{\frac{1}{N}}(1 - 2^{\frac{N-1}{N}})}{1-2^{\frac{1}{N}}}\]
using the formula for the sum of a geometric progression.
The whole expression can now be written as
\[\dfrac{1}{2N} \left[3 + 2 \left( \dfrac{2^\frac{1}{N}(1-2^{\frac{N-1}{N}})}{1-2^{\frac{1}{N}}}\right )\right].\]
There are many ways to rearrange this expression, but three answers have a \(1\) in them, so we can use that as a starting point.
So the answer is (b).

