into a subset of the positive real numbers. Derive the trapezium rule for the approximate evaluation of the area under the curve \(y = f(x)\) between \(x=a\) and \(x=b\), using \((n-1)\) points of subdivision at a distance \(h = (b-a)/n\) apart.
Consider the following diagram.
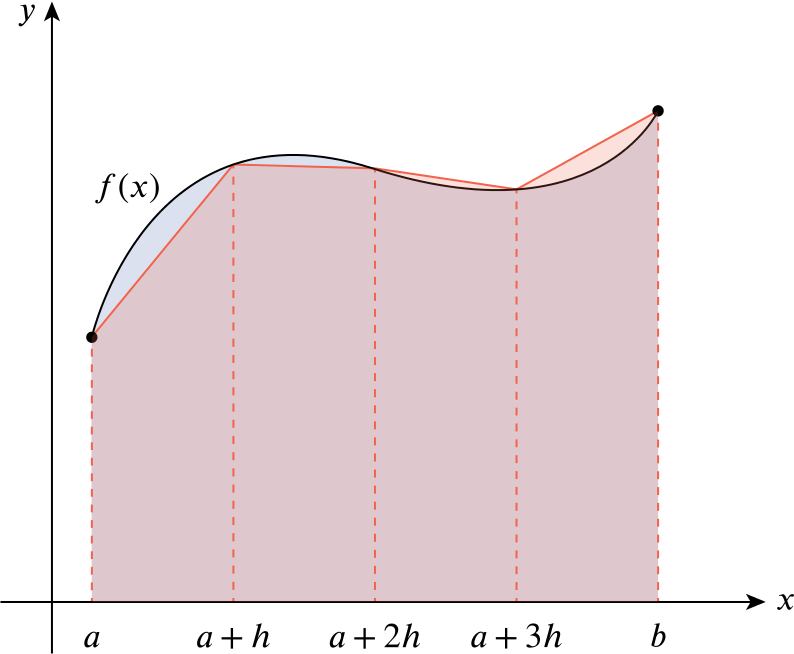
In this diagram, we start with the graph of \(y = f(x)\) between \(x=a\) and \(x=b\). This is shown in black. Our goal is to approximate the area under this curve; this is the region in blue (and purple, where it overlaps with the red region).
We then fix an integer \(n\), define \(h = (b-a)/n\), and divide the interval \(a \le x \le b\) into \(n\) equal parts (of length \(h\)) by marking the points at \(a+h\), \(a+2h\), and so on. We then draw line segments between \((a,f(a))\) and \((a+h,f(a+h))\); between \((a+h,f(a+h))\) and \((a+2h,f(a+2h))\); and so on. This is the (piecewise linear) curve in dark red.
The trapezium rule says that the area under the red curve (the region in light red; this is a sequence of trapezia) is approximately the same as the area under the original graph, with the approximation becoming more exact as \(n\) increases. We will write this symbolically: \[\begin{align*} &\text{area of the first trapezium} + \text{area of the second trapezium} + \dotsb + \text{area of the last trapezium}\\ &= \frac{f(a) + f(a+h)}{2} h + \frac{f(a+h) + f(a+2h)}{2} h + \dotsb + \frac{f(b-h) + f(b)}{2} h \\ &= \frac{h}{2} \left( f(a) + 2f(a+h) + 2f(a+2h) + \dotsb + 2f(b-h)+ f(b) \right) \\ &\approx \int_a^b f(x) \:dx. \end{align*}\]using the points of subdivision given in the following table:
| \(x\) | \(3.0\) | \(3.5\) | \(4.0\) | \(4.5\) | \(5.0\) |
| \(x \ln x\) | \(3.296\) | \(4.385\) | \(5.545\) | \(6.768\) | \(8.047\) |
We can, in fact, integrate \(x \ln x\) exactly using integration by parts. We find \(\int_3^5 x \ln x \:dx = 11.17421860\!\ldots\), so the above approximation is not bad.

