For a real number \(x\), we denote by \(\lfloor x \rfloor\) the largest integer less than or equal to \(x\). Let
\[f(x) =\dfrac{x}{2}-\left\lfloor \dfrac{x}{2} \right\rfloor.\]
The smallest number of equal width strips for which the trapezium rule produces an overestimate for the integral
\[\int_0^5 f(x) \:dx\]
is
(a) \(2,\quad\) (b) \(3,\quad\) (c) \(4,\quad\) (d) \(5,\quad\) (e) it never produces an overestimate.
If we sketch the graph for \(0 \leq x \leq 5\), we find that it takes a saw-tooth shape.
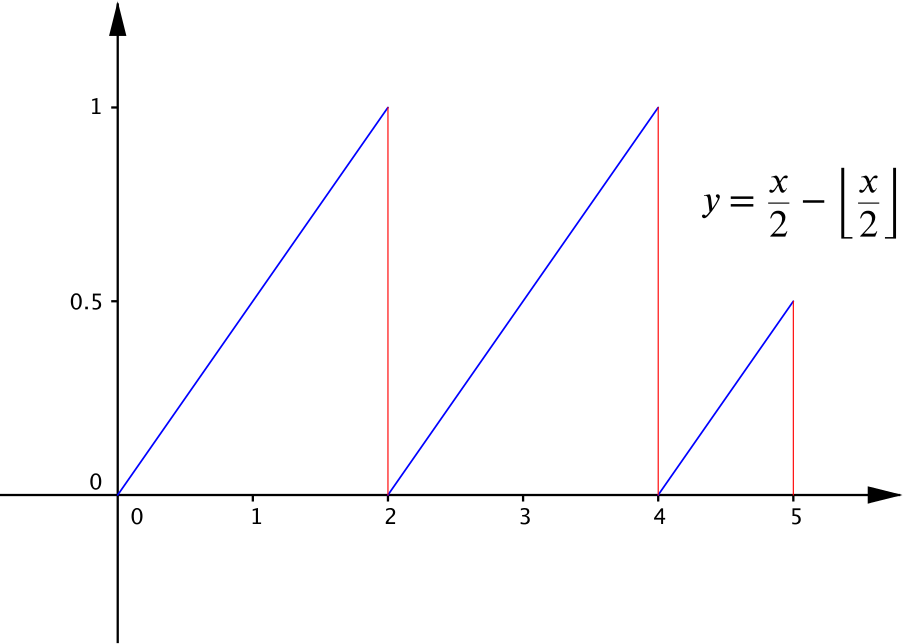
It’s easy to calculate the integral; it is the area of the three triangles shown, which is \(\dfrac{9}{4}\).
What happens if we apply the trapezium rule with two strips?
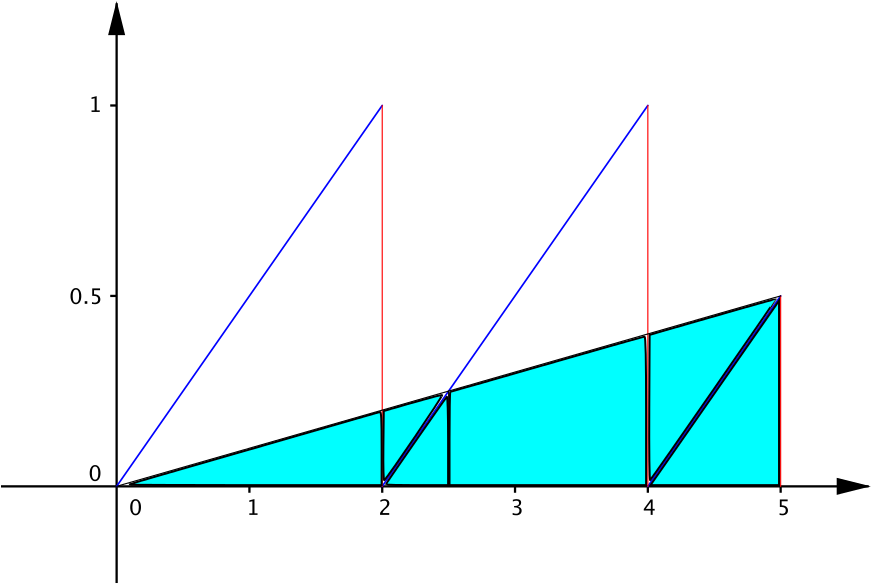
The trapezium rule returns the area of the blue triangle, which is \(\dfrac{5}{4} < \dfrac{9}{4}\), an underestimate.
What happens with three strips?
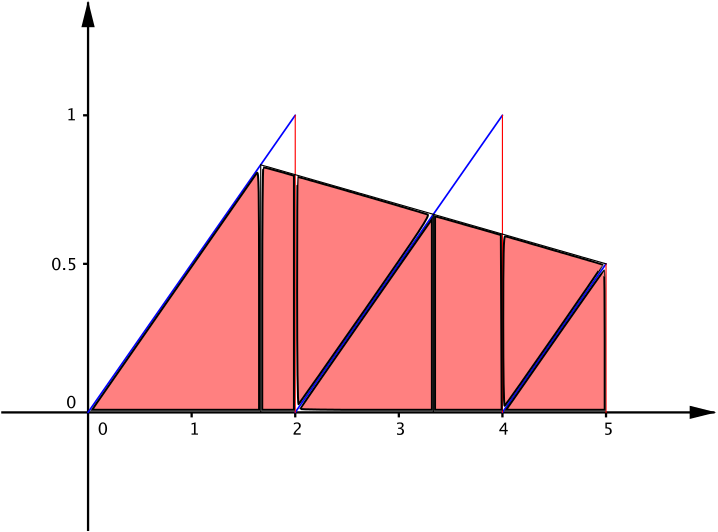
By the trapezium rule, the shaded area now is \(\dfrac{1}{2}\times\dfrac{5}{3}\left[0+\dfrac{1}{2}+2\left(\dfrac{5}{6}+ \dfrac{2}{3}\right)\right] = \dfrac{105}{36}> \dfrac{9}{4}\), and so the answer is (b).
If we apply the trapezium rule with \(5n\) strips, where \(n\) is a positive integer, the result agrees exactly with the given integral.

