The equation of a curve is \[ y = \cot x - 8 \cos x, \quad (0 < x < \pi). \] Find the coordinates of the points on the curve where \(\dfrac{dy}{dx} = 0\).
Using \(\cot x=\dfrac{1}{\tan x}\) will give us problems at \(x=\dfrac{\pi}{2}\), so we’ll use the alternative, \[ \cot x = \frac{\cos x}{\sin x}. \]
We can differentiate \(y\): \[ \frac{dy}{dx} = \frac{d}{dx}(\cot x) + 8\sin x. \] What’s the derivative of \(\cot x\)? It’s \(-\cosec^2 x\).
So we have that \[\frac{dy}{dx} = -\cosec^2 x + 8\sin x.\]
Now \[\begin{align*} -\cosec^2 x + 8\sin x &=0\\ \iff 8 \sin x &= \cosec^2 x\\ \iff (\sin x)^3 &= \dfrac{1}{8}\\ \iff \sin x &= \dfrac{1}{2}.\\ \end{align*}\]We’re allowed to multiply both sides by \(\sin^2 x\) in the above, since \(\sin x\) is not zero for \(0 < x < \pi\).
Solutions for \(x\) in the given range are \(\dfrac{\pi}{6}\) and \(\pi - \dfrac{\pi}{6} = \dfrac{5\pi}{6}\).
We were asked, however, to find the coordinates of the stationary points. The first is \[ \left( \frac{\pi}{6}, \frac{\cos \tfrac{\pi}{6}}{\sin \tfrac{\pi}{6}} - 8 \cos \frac{\pi}{6} \right) = \Biggl( \frac{\pi}{6}, \frac{\tfrac{\sqrt{3}}{2}}{\tfrac{1}{2}} - 8 \frac{\sqrt{3}}{2} \Biggr) = \left( \frac{\pi}{6}, -3\sqrt{3} \right) \] and the second is \[ \left( \frac{5\pi}{6}, \frac{\cos \tfrac{5\pi}{6}}{\sin \tfrac{5\pi}{6}} - 8 \cos \frac{5\pi}{6} \right) = \Biggl( \frac{5\pi}{6}, \frac{-\tfrac{\sqrt{3}}{2}}{\tfrac{1}{2}} + 8 \frac{\sqrt{3}}{2} \Biggr) = \left( \frac{5\pi}{6}, 3\sqrt{3} \right). \]
Sketch the curve.
Now we have the coordinates of the stationary points, we can think about the sketch. First we should think about what happens as \(x \to 0\) and \(x \to \pi\):
As \(x \to 0\), \(\dfrac{\cos x}{\sin x} \to + \infty\), and \(- 8 \cos x \to -8\), so \(y \to + \infty\)
As \(x \to \pi\), \(\dfrac{\cos x}{\sin x} \to - \infty\), and \(- 8 \cos x \to 8\), so \(y \to - \infty\)
So since there are only two stationary points, and we have their coordinates, there is really only one shape the curve can have. So we have the beginnings of our sketch:
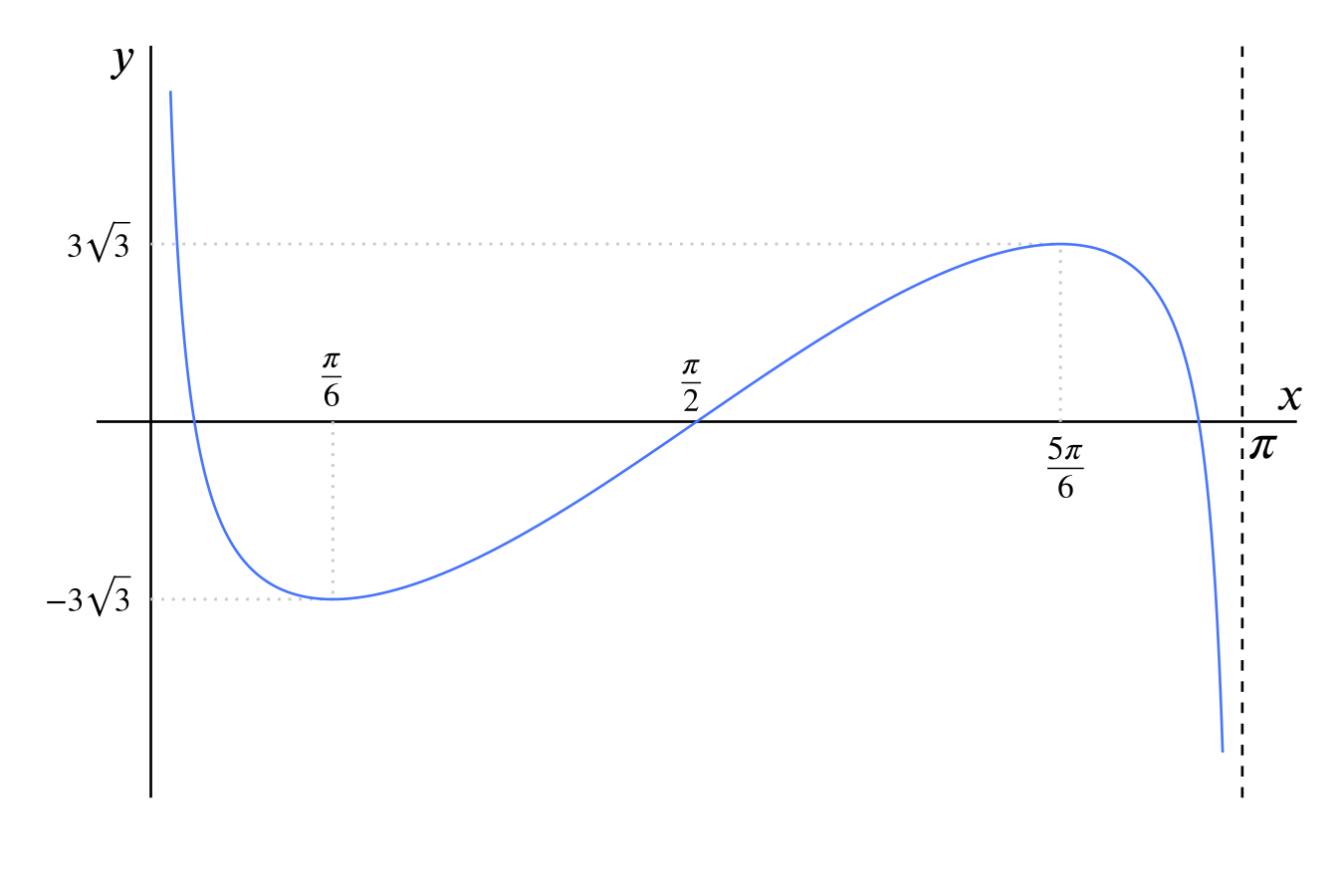
Now all we need to do is find the points where the graph crosses the \(x\)-axis, in the range given. We can factorise \(y\) as
\[y = \cos x \left( \dfrac{1}{\sin x} - 8 \right),\]
so \(y = 0\) if and only if either \(\cos x = 0\) or \(\sin x = \dfrac{1}{8}\), which in turn happens only when \(x\) takes one of the three values
\[\dfrac{\pi}{2}, \quad \sin^{-1}{\tfrac{1}{8}}, \quad \pi - \sin^{-1}{\tfrac{1}{8}}\]
We can see \(\dfrac{\pi}{2}\) is in the middle of the range, and if we calculate \(\sin^{-1}{\tfrac{1}{8}}\) we can see that it is less than \(\dfrac{\pi}{6}\) which is where our first turning point occurs. So the first \(x\)-intercept does indeed occur where we thought it did, looking back at our preliminary sketch. And this in turn implies that \(\pi - \sin^{-1}{\tfrac{1}{8}} > \dfrac{5 \pi}{6}\)
So we can mark on our intercepts, and our sketch is done!
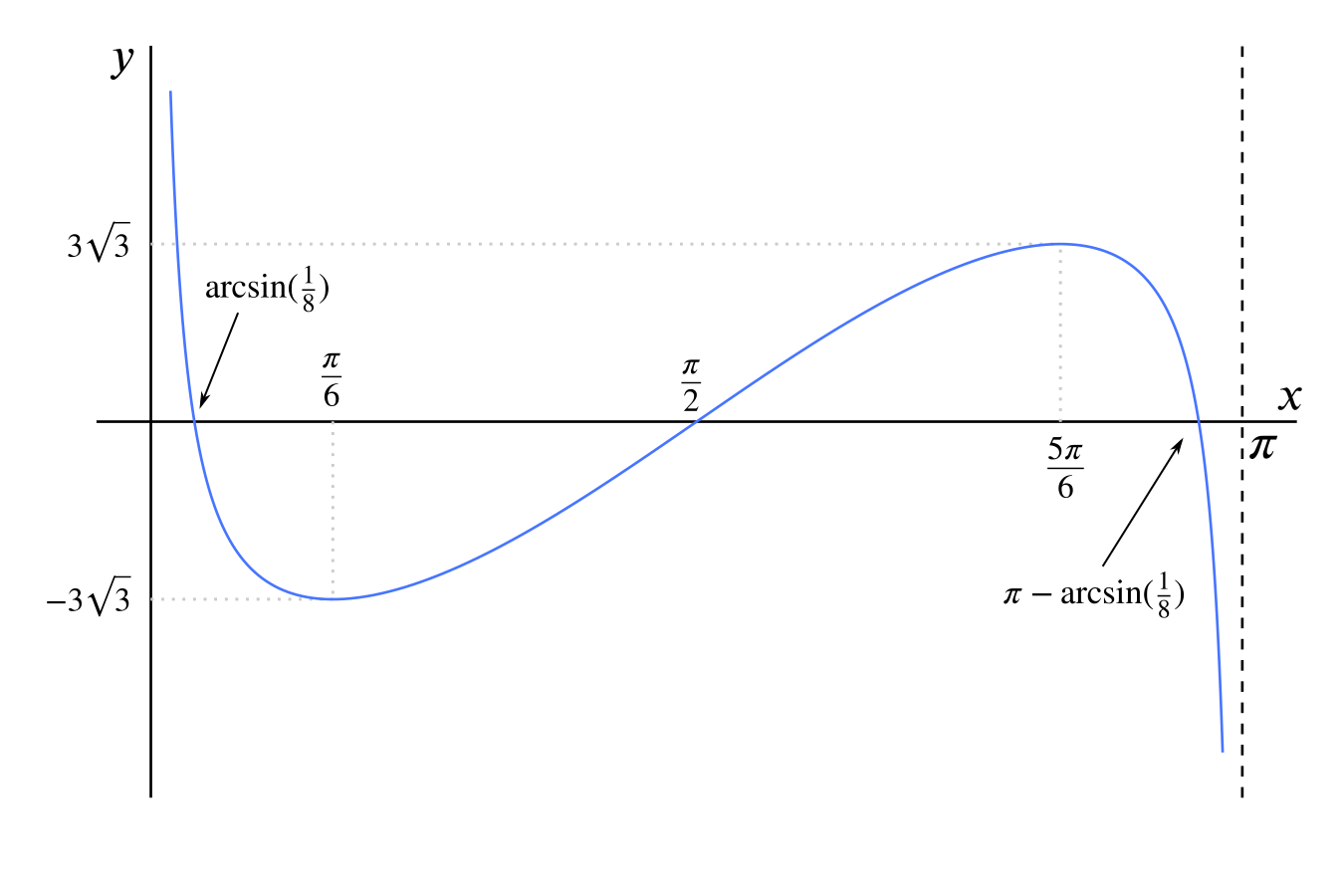
Note that the curve has rotational symmetry around the point \(\left(\dfrac{\pi}{2}, 0\right)\). This is to be expected since both \(\cos x\) and \(\cot x\) have the same symmetry.

