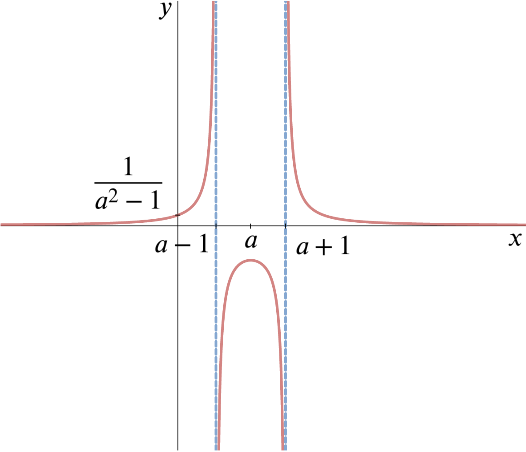
- Sketch the curve \(y=f(x)\) where \[f(x)=\frac{1}{(x-a)^2-1} \qquad \qquad (x\neq a\pm 1),\] and \(a\) is a constant.
Using the difference of two squares, \((x-a)^2 - 1 = ((x-a)-1)(x-a)+1) = (x-(a+1))(x-(a-1))\).
Thus \(f(x) = \dfrac{1}{(x-(a+1))(x-(a-1))}\), and we have the vertical asymptotes \(x = a-1\) and \(x = a+1\).
Near the asymptote \(x=a-1\) as \(x \rightarrow a-1\) from below \((x-a)^2 \rightarrow 0\) from above so \(f(x) \rightarrow \infty\), whereas above \(x=a-1, \: \: f(x) \rightarrow -\infty\).
Similarly near the asymptote \(x=a+1\) as \(x \rightarrow a+1\) from below \((x-a)^2 \rightarrow 0\) from below so \(f(x) \rightarrow -\infty\), whereas above \(x=a+1, \: \: f(x) \rightarrow \infty\).
As \(x \rightarrow \infty, \: \: f(x)\) is positive and tending to zero, and as \(x \rightarrow -\infty, \: \: f(x)\) is also positive and tending to zero.
We have the \(y\)-intercept when \(x=0\): \[f(0)=\frac{1}{a^2-1}.\]
There are no roots to the equation \(f(x)=0\), and we can see that the curve will be symmetrical about the line \(x=a\).
We can use the symmetry about \(x=a\) to find the maximum point of the central branch by evaluating the curve at \(x=a\) giving \(f(a)=-1\).
We could look for turning points by setting the first derivative equal to zero. To find the first derivative we will need to use quotient rule: \[0=f'(x)=-\frac{2(x-a)}{((x-a)^2-1)^2}\] \[\iff \quad 2(x-a)=0.\] So the only stationary point is at \(x = a\), and \(f(a) = -1\).
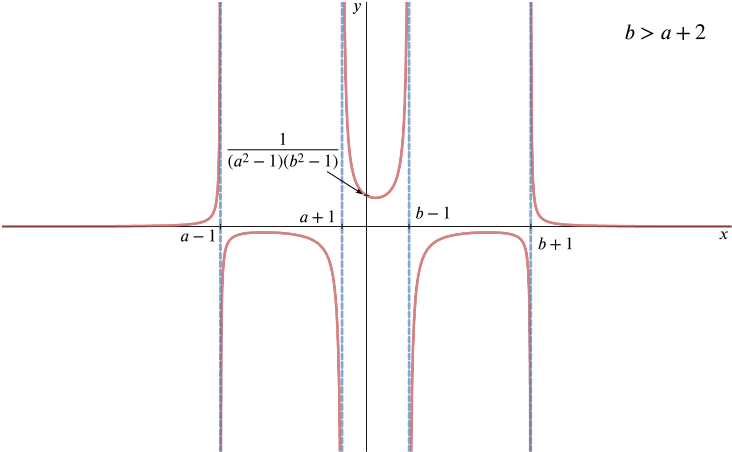
- The function \(g(x)\) is defined by \[g(x)=\frac{1}{((x-a)^2-1)((x-b)^2-1)} \qquad \qquad (x\neq a\pm 1,\,x\neq b \pm 1),\] where \(a\) and \(b\) are constants, and \(b>a\). Sketch the curves \(y=g(x)\) in the two cases \(b>a+2\) and \(b=a+2\), finding the values of \(x\) at the stationary points.
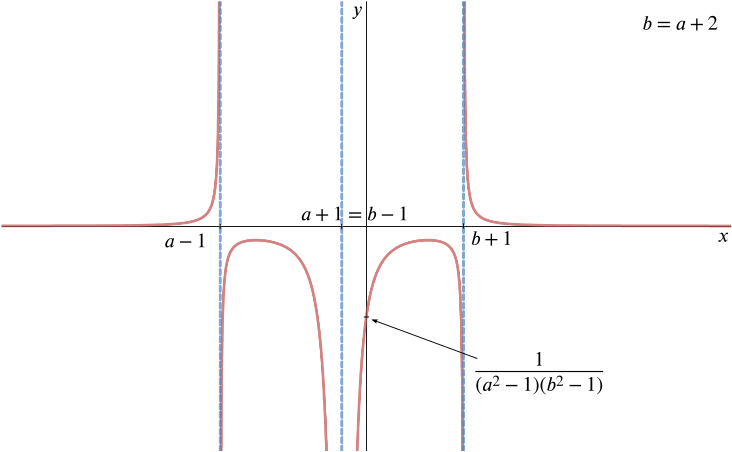
We have \(g(x) = \dfrac{1}{(x-(a+1))(x-(a-1))(x-(b-1))(x-(b+1))}\), as before.
Thus we have the vertical asymptotes \(x = a-1, x = a+1, x = b-1\) and x = \(b+1\).
If \(b > a+2\), these will be distinct, with \(x = b-1\) and x = \(b+1\) being to the right of the first two.
As \(x \rightarrow \infty, \: \: f(x)\) is positive and tending to zero, and as \(x \rightarrow -\infty, \: \: f(x)\) is also positive and tending to zero.
The \(y\)-intercept is \[g(0)=\frac{1}{(a^2-1)(b^2-1)},\] and again there are no roots of \(g(x)=0\). This time, the curve will be symmetric about \(x=\frac{1}{2}(a+b)\).
Stationary points occur when \(g'(x)=0\) so \[0=g'(x)=\frac{-2(x-a)}{((x-a)^2-1)^2((x-b)^2-1)}+\frac{-2(x-b)}{((x-a)^2-1)((x-b)^2-1)^2}\] \[\begin{align*} \iff 0&= (x-a)[(x-b)^2-1]+(x-b)[(x-a)^2-1]\\ &=(x-a)^2(x-b)-(x-b)+(x-a)(x-b)^2-(x-a)\\ &=(x-a)(x-b)\left[(x-a)+(x-b)\right]-\left[(x-a)+(x-b)\right] \\ &=\left((x-a)(x-b)-1\right)(2x-a-b) \end{align*}\] \[\iff [x^2-(a+b)x+(ab-1)](2x-a-b)=0.\] The roots of this are therefore \[\begin{align*} x&=\frac{1}{2}(a+b)\\ \text{and } x &= \frac{(a+b)\pm\sqrt{(a+b)^2-4(ab-1)}}{2}\\ &=\frac{(a+b)\pm\sqrt{a^2-2ab+b^2+4}}{2}\\ &=\frac{1}{2}(a+b)\pm\frac{1}{2}\sqrt{(a-b)^2+4}. \end{align*}\]The discriminant of this is always positive so these two roots are found equally spaced either side of the first root \(x=\frac{1}{2}(a+b)\).
We can see that \[g\left(\frac{1}{2}(a+b)\right)=\frac{1}{\left(\frac{1}{4}(b-a)^2-1\right)\left(\frac{1}{4}(a-b)^2-1\right)}=\frac{1}{\left(\frac{1}{4}(b-a)^2-1\right)^2}>0.\]
When \(b>a+2\), we have \(b-1>a+1\) so there are four distinct asymptotes and the sketch is
When \(b=a+2\), we have \(b-1=a+1\) so we lose the middle branch and the sketch is