Show that, if \(y=\dfrac{x^2+1}{x^2-a^2},\) \(y\) takes all real values twice, except those for which \(-\dfrac{1}{a^2}\le y\le 1\).
Since \(y\) is a function of \(x^2\) rather than just \(x\) we can show that in general \(y(x)=y(-x)\) by substituting and simplifying:
\[\begin{align*} y(-x)&=\dfrac{(-x)^2+1}{(-x)^2-a^2} \\ &=\dfrac{x^2+1}{x^2-a^2}\\ &=y(x). \end{align*}\]This tells us that where \(y\) exists and \(x \neq -x\) then \(y\) values are repeated.
As \(x \rightarrow a \quad x^2-a^2 \rightarrow 0\) so \(y \rightarrow \pm \infty\).
Since \(x^2+1\geq1 \quad y\neq 0\) so there are some values that \(y\) cannot take and we must find them.
Rearranging \(y=\dfrac{x^2+1}{x^2-a^2}\), we arrive at \[x^2=\dfrac{a^2y+1}{y-1}.\]
Since \(x\) is real \(x^2 \geq 0\) so a \(y\)-value is impossible if and only if \(\dfrac{a^2y+1}{y-1} < 0\).
So when is \(\dfrac{a^2y+1}{y-1} < 0\)?
If \(y-1\) is positive, then \(a^2y+1<0 \implies y < -\dfrac{1}{a^2}\), which is impossible, since \(y > 1\).
On the other hand, if \(y-1\) is negative (that is if \(y<1\)), then \(a^2y+1>0 \implies y > -\dfrac{1}{a^2}\), so we have \(-\dfrac{1}{a^2}<y<1\).
If \(y = 1\), then no \(x\)-values are possible. If \(y = -\dfrac{1}{a^2}\), then \(x = 0\), but this \(y\)-value (occurring at the \(y\)-intercept) is unique (not repeated) and is the position we noted earlier when \(x=-x\).
This means that \(y\) takes each real value twice, except when \(-\dfrac{1}{a^2}\le y\le 1\).
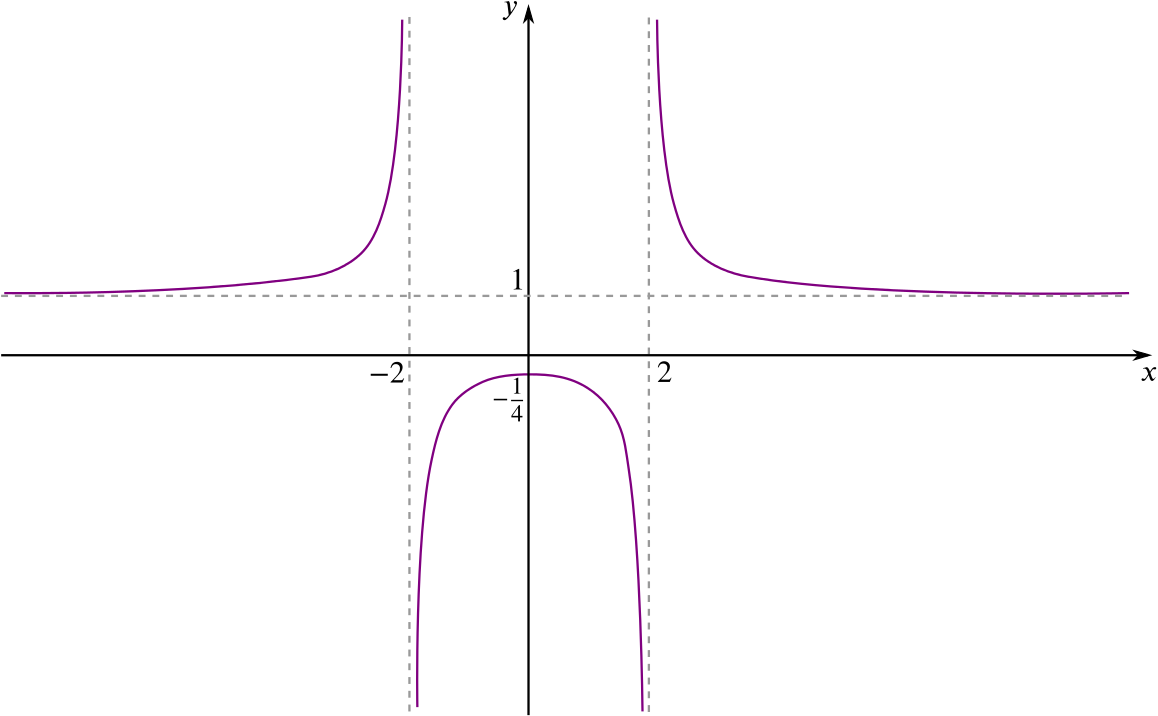
Sketch the curve \(y=\dfrac{x^2+1}{x^2-4}\), indicating its asymptotes.
Since \(y(x) = y(-x)\), the graph is symmetrical about the \(y\)-axis (this is an even function). We have vertical asymptotes at \(x = \pm a\).
We can calculate the derivative of \(y\): \[\frac{dy}{dx}=\frac{2x}{x^2-a^2}-\frac{2x(x^2+1)}{(x^2-a^2)^2}=\frac{2x(x^2-a^2-x^2-1)}{(x^2-a^2)^2}=-\frac{2(a^2+1)x}{(x^2-a^2)^2}.\]
We see that \(y\) has a stationary point at \(x=0\).
Moreover, \(y\) is decreasing for positive \(x\), and increasing for negative \(x\), (except at \(\pm a\), where the derivative is undefined).
This tells us that \(\left(0, -\dfrac{1}{a^2}\right)\) is a local maximum. Also, we can rewrite \(y\) as \[y=\frac{x^2+1}{x^2-a^2}=\frac{x^2-a^2+1+a^2}{x^2-a^2}=1+\frac{1+a^2}{x^2-a^2},\] and so \(y\) tends to \(1\) as \(x \to \pm \infty\). This all enables us to sketch the curve \(y=\dfrac{x^2+1}{x^2-4}\), as below.