\(P\) is a point on the circumference of a circle \(X\) of diameter \(\quantity{3}{in.}\) . An arc of another circle \(Y\) is drawn with centre \(P\), intersecting \(X\) at \(Q\) and \(R\). Express the lengths of \(PQ\) and the minor arc \(QR\) of \(Y\) in terms of \(\theta\), where \(\theta\) is the angle, in radians, between \(PQ\) and the diameter of \(X\) through \(P\).
Here’s a diagram of the two circles \(X\) and \(Y\).
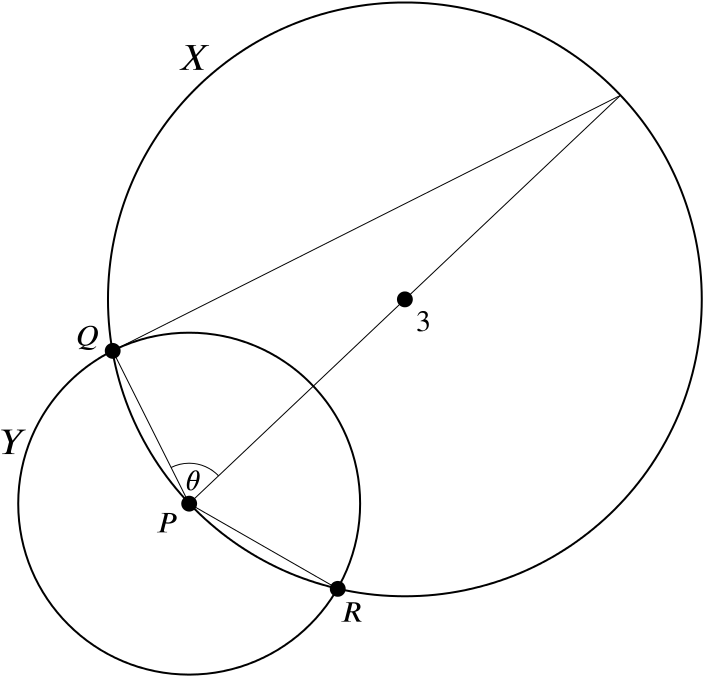
If you drew your circle \(Y\) larger than your circle \(X\), your diagram will look quite different to this: there’s no need to worry, the mathematics works just the same.
You can explore different versions of the diagram with this interactive:
We’ll calculate the two lengths in turn. Firstly, to find \(PQ\), let’s look at the circle \(X\).
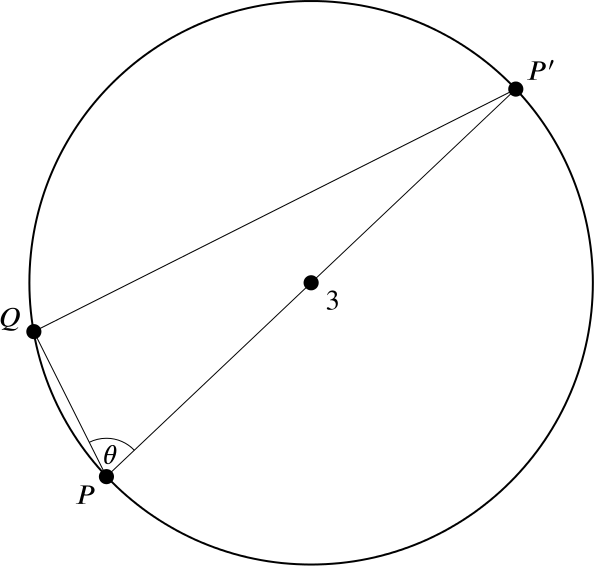
Since the angle \(PQP'\) lies in a semicircle, it must be a right angle. Now, from trigonometry, \[ \cos \theta = \frac{\text{adjacent}}{\text{hypotenuse}} = \frac{\text{length of $PQ$}}{\text{length of $PP'$}} \implies \text{length of $PQ$} = 3 \cos \theta. \]
Secondly, to find the length of the minor arc \(QR\), let’s look at the circle \(Y\).

The length of an arc of a circle is \(r\phi\), where \(\phi\) is the angle subtended at the centre of the circle by the arc.
By symmetry, \(\angle QPR = \theta + \theta = 2\theta\), and so the length of the minor arc \(QR\) is \(PQ \times 2\theta = 6\theta\cos\theta.\)
Prove that the length of the arc \(QR\) has a stationary value when \(\theta = \cot \theta\), and that this value is a maximum.
We know that \[ QR = 6 \theta \cos \theta. \] Using the product rule, we have \[ \dfrac{d(QR)}{d\theta}= 6\theta (-\sin \theta) + 6\cos \theta = 6 (\cos \theta - \theta \sin \theta). \]
So the stationary points are those values of \(\theta\) for which \[ \cos \theta = \theta \sin \theta, \] which is true if and only if \[\theta = \cot \theta.\]
We can divide through here by \(\sin \theta\), since \(\theta = 0\) is not going to be a solution to our equation.
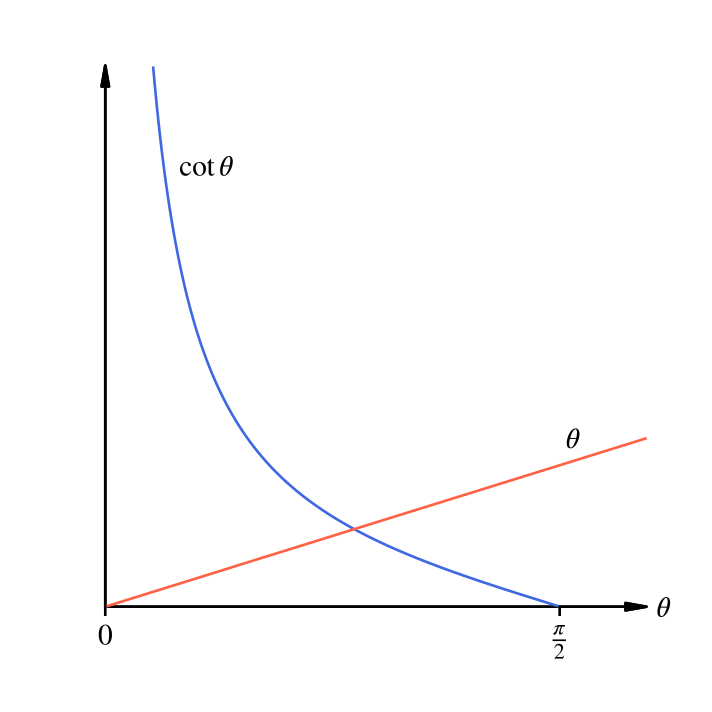
We are only concerned with the interval \(0 \le \theta \le \dfrac{\pi}{2}\).
Since \(\theta\) increases from zero and \(\cot \theta\) descends from infinity, as illustrated below, our equation has just one solution.
Is this a maximum? We know that \(QR > 0\) when \(0 < \theta < \dfrac{\pi}{2}\), that \(QR = 0\) when \(\theta = 0\) and \(\dfrac{\pi}{2}\), and that there’s only one stationary point between \(0\) and \(\dfrac{\pi}{2}\); therefore, this point has to be a maximum.
We can see this in the changing values in the GeoGebra illustration above.
If we try dragging \(R\), what happens to \(QR\)? For what value of \(\theta\) is this a maximum? Does \(\theta = \cot \theta\) here?
Alternatively, we could calculate the second derivative \(f''(\theta)\) and check that it’s negative on this interval.

