Can we show the function $(2x+1)/(x^2-1)$ can take all real values?

Add to your resource collection Remove from your resource collection Add notes to this resource View your notes for this resource

Let \(y=\dfrac{2x+1}{x^{2}-1}\) (\(x \neq \pm 1\)). Rearranging, we have that \[yx^2-2x-(1+y)=0.\] We can solve this quadratic for \(x\) to find that (if \(y \neq 0\)), \[\begin{align*} x &= \frac{2\pm\sqrt{4+4y(y+1)}}{2y}\\ &= \frac{1 \pm \sqrt{y^2 + y + 1}}{y}\\ &=\frac{1 \pm \sqrt{\left(y+\frac{1}{2}\right)^2 + \frac{3}{4}}}{y}. \end{align*}\]

So for any value of \(y\neq 0\), this gives real values for \(x\), and so for these \(x\)-values, \[f(x)=\frac{2x+1}{x^2-1} = y.\]

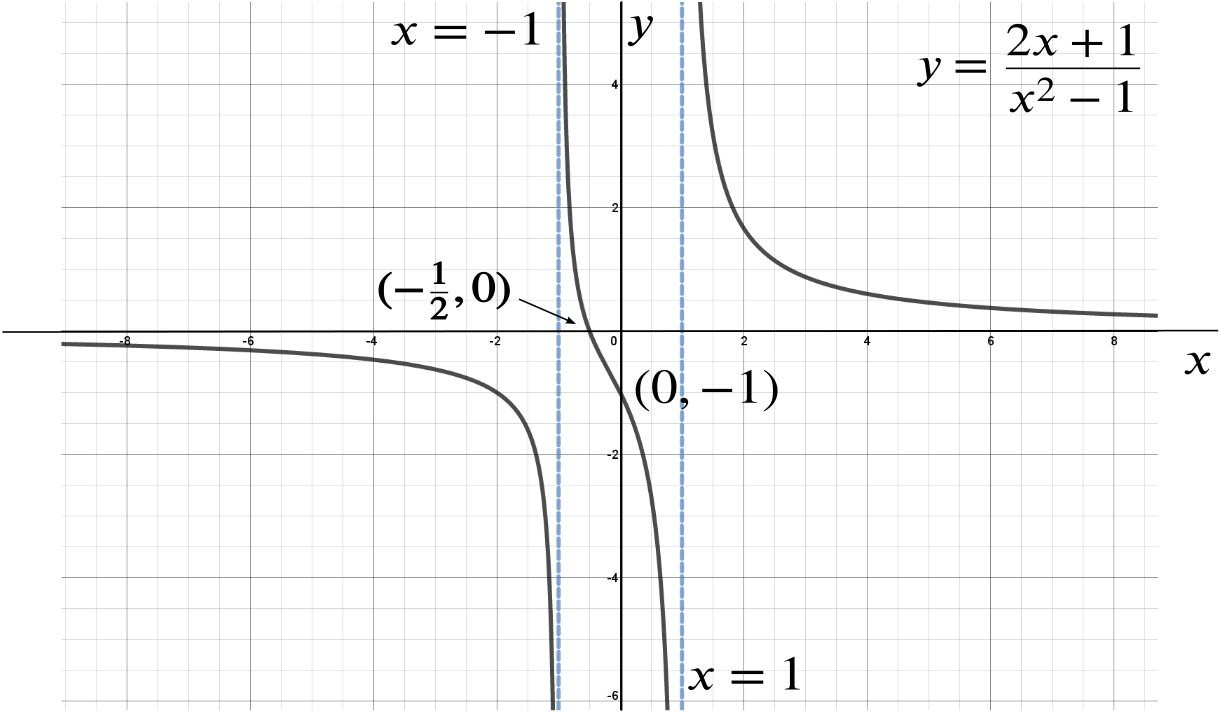
If \(y = 0\), then \(x = -\dfrac{1}{2}\) gives \(f(x) = y\). So the function takes all real values.

There are vertical asymptotes at \(x=\pm 1\), and the curve behaves like \(y=\dfrac{2}{x}\) for large \(x\).

Also \(f(0)=-1\) and the only root for \(f(x) = 0\) is \(-\frac{1}{2}\).

We can find the gradient of the curve by using the quotient rule (\(x \neq \pm 1\)): \[\begin{align*} f'(x) &= \frac{2(x^2-1)-(2x+1)(2x)}{(x^2-1)^2}\\ &= \frac{-2x^2-2x-2}{(x^2-1)^2}\\ &= \frac{-2(x^2+x+1)}{(x^2-1)^2}\\ &= \frac{-2\left(\left(x+\frac{1}{2}\right)^2+\frac{3}{4}\right)}{(x^2-1)^2},\\ \end{align*}\]

which is always negative.

A point of inflection on a curve occurs where the gradient function has a maximum or a minimum.

Informally, our curve must change from being concave upwards to concave downwards in between the two asymptotes \(x\pm1\), and so it has a point of inflection somewhere there.

To be sure of this, we note that \(f'(-0.5) = -\dfrac{24}{9}\), \(f'(0) = -2\), \(f'(0.5) = -\dfrac{56}{9}\), and that \(-\dfrac{24}{9} < -2 > -\dfrac{56}{9}\).

This means, if we imagine the graph of \(y=f'(x)\), a continuous function between \(-1\) and \(1\), that \(f'(x)\) must have a local maximum between \(-0.5\) and \(0.5\).