If \(y=\dfrac{e^{-x}}{1+x^2}\), prove that (i) \(y\) is always positive, …
We know \(e^x > 0\) for every \(x\), so \(e^{-x}\) has to be always positive too. We also know \(x^2\geq 0\), so \(\dfrac{1}{1+x^2}\) must be always positive.
The product of two positive numbers is also positive, and so \[\dfrac{e^{-x}}{1+x^2}>0,\] for every value of \(x\).
…, (ii) \(\dfrac{\mathrm{d}y}{\mathrm{d}x}\) is never positive.
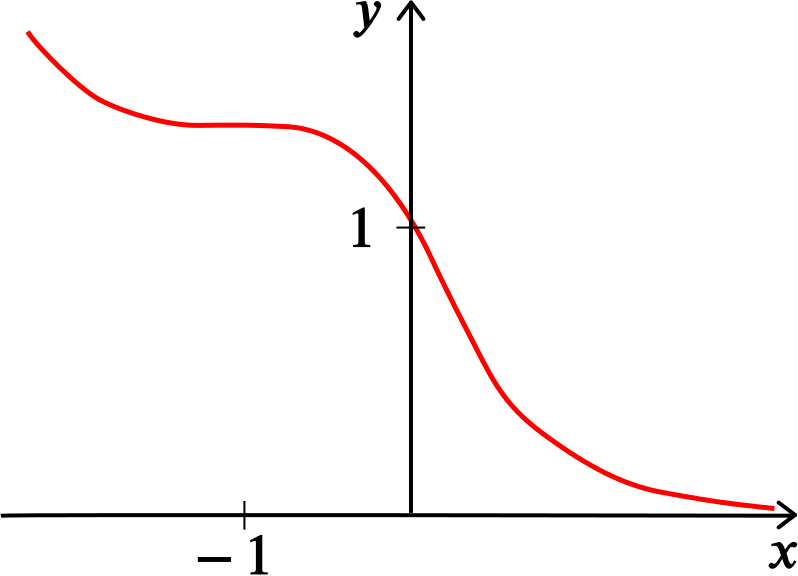
Find the coordinates of the point where \(\dfrac{\mathrm{d}y}{\mathrm{d}x}=0\), and sketch the graph of the function.
We can see that \(y' = 0 \implies x = -1, y = \dfrac{e}{2}.\)
Since \(y' \leq 0\), we know the function is never-increasing, so this point isn’t a maximum or a minimum, and must be a point of inflection.
To sketch the function, it’s useful to calculate a few more characteristics.
We have that the point \((0,1)\) is on the curve; we know from the question that \(y \to \infty\) as \(x \to -\infty\), and we can see that \(y \to 0\) for \(x \to \infty\).