Expressions collection
\(\dfrac{4}{x} - \dfrac{3}{x-2}\)
\(\dfrac{4x}{5} + \dfrac{8x}{15} - \dfrac{1}{2}\)
\(x - \dfrac{5}{x -2} - \dfrac{5}{x+2}\)
\(\dfrac{x}{x+1} + \dfrac{2x}{x-3} + \dfrac{x^3 - 2x^2 - 11x}{(x-3)(x+1)}\)
- \[\begin{align*} \dfrac{4}{x} - \dfrac{3}{x-2} &= \dfrac{4(x-2)}{x(x-2)} - \dfrac{3x}{x(x-2)}\\ &= \dfrac{4x-8 - 3x}{x(x-2)}\\ &= \dfrac{x-8}{x(x-2)} \end{align*}\]
To test your solution, you could substitute a value into the original and simplified expressions to check they are the same.
Are there any values that you shouldn’t choose to substitute into the expressions? Why?
- \[\begin{align*} \dfrac{4x}{5} + \dfrac{8x}{15} - \dfrac{1}{2} &= \dfrac{24x}{30} + \dfrac{16x}{30} - \dfrac{15}{30}\\ &= \dfrac{24x+16x-15}{30}\\ &= \dfrac{8x - 3}{6} \end{align*}\]
To add the fractions, we chose the lowest common denominator. When we obtained a single fraction, we also found that we could cancel the common factor of \(5\). Both of these will help with simplifying and will often save work.
- \[\begin{align*} x - \dfrac{5}{x -2} - \dfrac{5}{x+2} &= \dfrac{x(x-2)(x+2)}{(x-2)(x+2)} - \dfrac{5(x+2)}{(x -2)(x+2)} - \dfrac{5(x-2)}{(x-2)(x+2)}\\ &= \dfrac{x^3 - 4x - 5x - 10 - 5x + 10}{(x - 2)(x+2)}\\ &= \dfrac{x(x^2-14)}{(x-2)(x+2)} \end{align*}\]
Here we might have noticed that there is a common factor of \(x\) in the numerator that means it can be factorised. Why do you think it might be helpful to factorise expressions?
- \[\begin{align*} \dfrac{2x}{x-3} - \dfrac{x}{x+1} + \dfrac{6-10x}{(x-3)(x+1)} &= \dfrac{2x^2+2x}{(x-3)(x+1)} - \dfrac{x^2 - 3x}{(x+3)(x-1)} + \dfrac{6-10x}{(x-3)(x+1)}\\ &= \dfrac{x^2 - 5x + 6}{(x-3)(x+1)}\\ &= \dfrac{(x-3)(x-2)}{(x-3)(x+1)}\\ &= \frac{x-2}{x+1} \end{align*}\]
By factorising the numerator we saw there was a common factor of \((x-3)\) that could cancel, so our final expression looks much simpler than the original.
Try substituting \(x=3\) into the original and simplified version. What happens? Why?
Having worked through these four questions, think about the following:
How did you use common factors to help you in these questions? How did this affect your answers?
What is the ‘simplest form’? Does it always mean writing fractions in a single term?
Equations collection
\(\dfrac{3}{x+3} - \dfrac{1}{x-4} + \dfrac{57}{(x+3)(x-4)} = 1\)
\(\dfrac{4x}{5} - \dfrac{52}{15} = \dfrac{8}{3x}\)
\(\dfrac{3x}{4} +\dfrac{2x^2}{5} = \dfrac{x}{2}\)
\(\dfrac{x^2 - 2x}{x - 4} = \dfrac{2x}{x - 4}\)
- \[\dfrac{3}{x+3} - \dfrac{1}{x-4} + \dfrac{57}{(x+3)(x-4)} = 1\]
We should always choose the lowest common denominator to reduce the work we have to do. In this case it will be \((x+3)(x-4)\).
Therefore the expression becomes,
\[\dfrac{3(x-4)}{(x+3)(x-4)} - \dfrac{(x+3)}{(x-4)(x+3)} + \dfrac{57}{(x+3)(x-4)} = 1,\]
which simplifies to
\[3x - 12 - x - 3 + 57 = x^2 - x - 12.\]
Rearranging this into a form we can solve leaves us with
\[x^2 - 3x - 54 = 0,\]
so the solutions are
\[x = 9 \text{ or } x = -6.\]
We can check we are correct by substituting \(x = 9\) and \(x =-6\) into the original equation.
- \[\dfrac{4x}{5} - \dfrac{52}{15} = \dfrac{8}{3x}\]
We could immediately divide both sides by \(4\), to remove the common factors, or we could rearrange to get
\[12x^2 - 52x - 40 = 0,\]
and then divide through by \(4\) to give
\[3x^2 - 13x - 10 = 0.\]
Therefore
\[x = 5 \text{ or } x = -\dfrac{2}{3}.\]
- \[\dfrac{3x}{4} +\dfrac{2x^2}{5} = \dfrac{x}{2}\]
Look at this potential solution to the problem:
\[\dfrac{15x+8x^2}{20} = \dfrac{10x}{20}\] \[15x+8x^2 = 10x\] \[15+8x = 10\] \[8x = -5\] \[x = -\dfrac{5}{8}\]
How does this solution compare with your approach?
This follows a similar approach to the question above, but what is the difference between them?
- \[\dfrac{x^2 - 2x}{x - 4} = \dfrac{2x}{x - 4}\]
We saw in the equation above that dividing through by a variable can lose us a solution so we won’t divide through by \(x\). Instead, look at these two methods. How do they compare with what you did?
Method 1
\[\begin{align*} \dfrac{x^2 - 2x}{x - 4} &= \dfrac{2x}{x - 4} \\ x^2 - 2x &= 2x \\ x^2 - 4x &= 0 \\ x(x-4) &= 0 \\ x = 0 \text{ or } x &= 4. \\ \end{align*}\]Method 2
\[\begin{align*} \dfrac{x^2 - 2x}{x - 4} - \dfrac{2x}{x - 4} &= 0\\ \dfrac{x^2 - 4x}{x-4} &= 0\\ \dfrac{x(x - 4)}{x-4} &= 0\\ x &= 0\\ \end{align*}\]Why do we have an extra solution in one of the methods? Is \(x = 4\) a solution of this equation?
What changes if the numerator in the original equation was \(x^2 - 3x\) rather than \(x^2 - 2x\)? Will we get the same answer with both methods this time?
We know from working with numbers that dividing anything by zero causes problems. We can see this if we try to solve \(3x = 7x\) by dividing by \(x\), or in the loss of the solution that was shown in part c.
If you substitute \(x = 4\) into each side of the equation at the beginning, you’ll see that neither side has a value that exists, as we would be dividing by zero. We clearly can’t work with things that don’t exist so we must specify that in this case, \(x \neq 4\).
If we started again with method \(1\), then we could multiply both sides by \(x - 4\) because as \(x \neq 4\), the denominator is not zero. Therefore when we get to \(x(x-4) = 0\), we already know \(x \neq 4\), so the only solution is \(x = 0\).
The same with method \(2\), when we reach the factors of \(x-4\) cancelling, we are not cancelling two zeros, because we have already stated \(x \neq 4\).
Inequalities collection
\(\dfrac{3(x-1)}{4} < \dfrac{5x-1}{2}\)
\(\dfrac{4x-3}{2} - \dfrac{2x+2}{5} ≥0\)
\(\dfrac{5}{3} - \dfrac{1}{x} < \dfrac{3}{x}\)
\(\dfrac{5x+6}{x-2} ≤ 2\)
- \[\dfrac{3(x-1)}{4} < \dfrac{5x-1}{2}\]
This can be solved by the following steps:
\[3x - 3 < 10x - 2\]
As with the expressions and equations, we can reduce our work if we multiply both sides by the lowest common denominator.
\[-1 < 7x\]
\[ x > -\dfrac{1}{7}.\]
It is more difficult to check your solutions to an inequality, as you cannot test all values. However you can choose some simple values e.g. \(x=0\), to check if they satisfy the inequality. This might give you some confidence your answer is correct.
If we rearranged the inequality in a different order, and ended up with the following statement,
\[-7x < 1,\]
what could the next step be in order to get the correct answer? Can you explain why?
- \[\dfrac{4x-3}{2} - \dfrac{2x+2}{5} ≥0\]
\[\dfrac{5(4x - 3)}{10} - \dfrac{2(2x+2)}{10} ≥ 0\]
\[20x - 15 - 4x - 4 ≥ 0\]
\[16x - 19 ≥0\]
\[x ≥ \dfrac{19}{16}.\]
- \[\dfrac{5}{3} - \dfrac{1}{x} < \dfrac{3}{x}\]
There are always many different routes we can take to solving an equation or inequality. For this question we may have approached it something like this.
\[\dfrac{5}{3} - \dfrac{1}{x} < \dfrac{3}{x}\]
\[\dfrac{5}{3} < \dfrac{4}{x}\]
\[5x < 12\]
\[x < \dfrac{12}{5}.\]
If we then took a value that is satisfied by this inequality, such as \(x = 1\), we would have found it satisfied the original inequality as well. However, if we took a different value such as \(x = -1\), then we would have found that it did not satisfy the original inequality.
What is happening here? Can you identify any steps in the working where there could be a problem?
How could we solve this inequality to be sure of the correct answer?
- \(\dfrac{5x+6}{x-2} ≤ 2\)
We might have attempted this question in a similar manner to the question above. If we did the following steps:
\[\dfrac{5x+6}{x-2} ≤ 2\]
\[5x + 6 ≤ 2x - 4\]
\[3x ≤ -10\]
\[x ≤ -\dfrac{10}{3}\]
then substituted in a value such as \(x = -4\), we would have found that it didn’t satisfy the original inequality. We could pick any value \(< -\dfrac{10}{3}\), but it will not work.
Something strange has happened in the last two questions. Techniques that we have used earlier have failed to solve these inequalities correctly.
What do you think the problem could be?
- \(\dfrac{5}{3} - \dfrac{1}{x} < \dfrac{3}{x}\)
We can simplify this inequality to
\[ \dfrac{5}{3} < \dfrac{4}{x}.\]
Is adding and subtracting to both sides always allowed?
This says that \(\frac{5}{3}\) is always smaller than \(\frac{4}{x}\). This can only be true when \(x\) is positive. So \(x >0\).
Solving the inequality as before gives us
\[x < \dfrac{12}{5}\]
so the whole solution is
\[ 0 < x < \dfrac{12}{5}.\]
In this case we were able to eliminate the possibility that \(x\) could be negative. What could we have done if we hadn’t been able to do this? Could we consider the two cases of \(x>0\) and \(x<0\)?
- \(\dfrac{5x+6}{x-2} ≤ 2\)
Unlike for c, we do not know anything about our value of \(x\). As \(x-2\) could be negative, we can’t multiply both sides by it.
Why can’t we multiply both sides by a value that could be negative?
Instead we can add or subtract.
\[\dfrac{5x+6}{x-2} - 2≤ 0\]
\[\dfrac{5x+6}{x-2} - \dfrac{2(x-2)}{x-2} ≤ 0\]
\[\dfrac{3x+10}{x-2} ≤ 0\]
We are now aware that we cannot multiply by \(x-2\) as it may be negative. Instead we need to think about what values this expression takes, and when it changes sign.
One way to do this is to look at the graph of the function \(y = \dfrac{3x+10}{x-2}\) and see when it is positive and when it is negative.
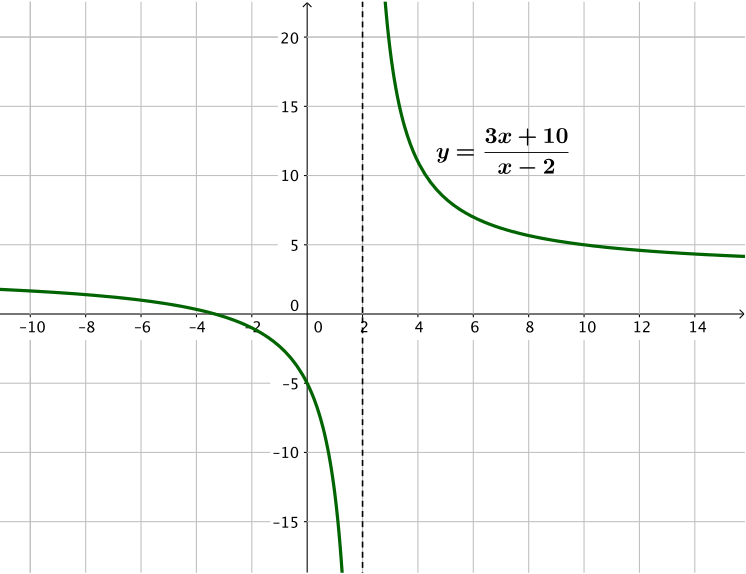
We can see from the graph that there is a root between \(x=-3\) and \(x = -4\), and the function changes from positive to negative either side of this. This is where the numerator is equal to zero and so \(x = -\dfrac{10}{3}\).
The graph has an asymptote at \(x=2\), i.e. the function cannot exist for this value of \(x\) as the denominator would be zero. The function changes from positive to negative either side of this value too.
We want to know when \(\dfrac{3x+10}{x-2} ≤ 0\), i.e. when it’s negative or zero.
So the solution is \(-\dfrac{10}{3} ≤ x < 2\).
Now you have finished try to think about the following questions:
What varies in your approach to each of the collections, for example, between simplifying expressions and solving equations?
Is cancelling by a common factor of 2 different from cancelling by a common factor of \(x-2\) when dealing with expressions/equations/inequalities?
What impact can multiplying or dividing by \(x\) (or a factor such as \(x+3\)) have?

