How might your thinking change if instead we had these two fractions?
\[\textrm{Fraction} \ C: \frac{10^c +1}{10^c -1} \qquad \textrm{Fraction} \ D: \frac{10^d + 1}{10^d -1}\]
For what values of \(c\) and \(d\) will fraction C be greater than fraction D?
If we take a step back and compare this pair of fractions to the first pair we will hopefully notice that it is only the denominators that have changed.
- The second term in each denominator has changed from \(+2\) to \(-1\).
How does this affect the value of the denominator?
In the first example the denominator was always positive. Is this still the case?
We might try to substitute values in place of \(c\) and \(d\) in order to get a sense of what is happening. There are four scenarios that we will need to consider:
What happens if both \(c\) and \(d\) are positive?
What happens if both \(c\) and \(d\) are negative?
What happens if just one of \(c\) or \(d\) is positive?
What happens if \(c\) or \(d\) is zero?
Now we might choose to take a similar approach as for the first pair of fractions. Re-writing this pair of fractions with a common denominator we have \[\textrm{Fraction} \ C: \frac{(10^c +1)(10^d - 1)}{(10^c -1)(10^d -1)} \qquad \textrm{Fraction} \ D: \frac{(10^d + 1)(10^c - 1)}{(10^d -1)(10^c - 1)}.\]
If either \(c\) or \(d\) is zero then the fractions are undefined (the denominator will be zero). For each of the other scenarios we might first consider whether or not the resulting fraction is positive or negative:
| Scenario | Sign of fraction \(C\) | Sign of fraction \(D\) | Conclusion |
|---|---|---|---|
| \(c>0\), \(d>0\) | \(\dfrac{(+)(+)}{(+)(+)}=+\) | \(\dfrac{(+)(+)}{(+)(+)}=+\) | Inconclusive |
| \(c<0\), \(d<0\) | \(\dfrac{(+)(-)}{(-)(-)}=-\) | \(\dfrac{(+)(-)}{(-)(-)}=-\) | Inconclusive |
| \(c>0\), \(d<0\) | \(\dfrac{(+)(-)}{(+)(-)}=+\) | \(\dfrac{(+)(+)}{(+)(-)}=-\) | Fraction \(C\) > Fraction \(D\) |
| \(c<0\), \(d>0\) | \(\dfrac{(+)(+)}{(-)(+)}=-\) | \(\dfrac{(+)(-)}{(-)(+)}=+\) | Fraction \(C\) < Fraction \(D\) |
This means that we only need to investigate the first two scenarios. In both cases the denominators will be positive and so we can consider the numerators alone: \[ \textrm{Numerator} \ C: (10^c + 1)(10^d - 1) = 10^{c+d} - 10^c + 10^d - 1\] and \[ \textrm{Numerator} \ D: (10^d + 1)(10^c - 1) = 10^{c+d} + 10^c - 10^d - 1.\]
As before, it is only the middle terms which differ so we consider this part of the numerator of \(C\): \[10^d - 10^c\] and the equivalent part of the numerator of \(D\): \[10^c - 10^d.\]
Now, if \(c>0\) and \(d>0\) then fraction \(C\) will be greater than fraction \(D\) when \(d>c\).
We should check this makes sense. If we take \(c=1\) and \(d=2\) then we get \[\textrm{Fraction} \ C: \frac{10^1 + 1}{10^1 - 1} = \frac{11}{9}\] and \[\textrm{Fraction} \ D: \frac{10^2 + 1}{10^2 - 1} = \frac{101}{99}.\]
We can use equivalent fractions to show that \(\dfrac{11}{9} > \dfrac{101}{99}\) and our solution holds.
If \(c<0\) and \(d<0\) then fraction \(C\) will again be greater than fraction \(D\) when \(d>c\).
Once again, we should check that this makes sense. If we take \(c=-2\) and \(d=-1\) then we get \[ \textrm{Fraction} \ C: \frac{10^{-2} + 1}{10^{-2} - 1} = -\frac{101}{99}\] and \[\textrm{Fraction} \ D: \frac{10^{-1} + 1}{10^{-1} - 1} = -\frac{11}{9}.\]
We can show that \(-\dfrac{101}{99} > -\dfrac{11}{9}\) and our solution holds.
A summary of our conclusions is below, relating the original scenarios proposed.
| Question | Answer |
|---|---|
|
Fraction \(C\) > Fraction \(D\) when \(d>c\) |
|
Fraction \(C\) > Fraction \(D\) when \(d>c\) |
|
Fraction \(C\) > Fraction \(D\) when \(c>0\) and \(d<0\) |
|
Fraction \(C\) or Fraction \(D\) respectively will be undefined. |
We might like to think of this problem graphically.
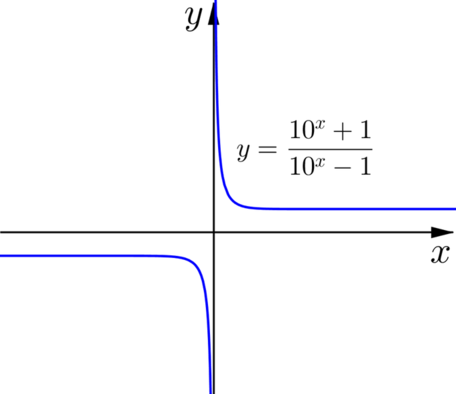
We can see that \(y=\dfrac{10^x + 1}{10^x - 1}\) is decreasing on the interval \((-\infty, 0)\) and also on \((0, \infty)\) (this is in contrast to the first problem in which the function was increasing).
Think about how each of the four questions posed above relates to regions of the graph.

