There are four separate square enclosures, three of side \(\quantity{x}{yd.}\) and one of side \(\quantity{y}{yd.}\) The sum of the areas of the enclosures is \(\quantity{147}{sq. yd.}\) and the sum of their perimeters is \(\quantity{96}{yd.}\) Obtain two equations containing \(x\) and \(y\) and solve them.
The area of a square of side \(x\) is \(x^2\), so the sum of the areas of the enclosures is \(3x^2 + y^2\).
Hence, our first equation is \(3x^2 + y^2 = 147\).
Now a square of side \(x\) has perimeter \(4x\), and so the sum of the perimeter of the enclosures is \((3 \times 4x) + 4y\).
Our second equation therefore is \(12x + 4y = 96\).
In order to solve these, we’ll now use the second equation to express \(y\) in terms of \(x\). Rearranging, we get
\[\begin{align*} 3x + y &= 24 \\ \implies y &= 24 - 3x. \end{align*}\]If we substitute this into the area equation above, we have
\[\begin{align*} 3x^2 + (24 - 3x)^2 &= 147 \\ \implies 3x^2 + 576 - 144x + 9x^2 &= 147 \\ \implies 12x^2 - 144x + 429 &= 0\\ \implies 4x^2-48x+143=0\\ \implies (2x-13)(2x-11)=0\\ \implies x = 5.5, 6.5. \end{align*}\]Alternatively we could use the quadratic equation formula to solve here, to get the two solutions for \(x\) given by
\[\begin{align*} x & = \frac{144 \pm \sqrt{144^2 - 4 \times 12 \times 429}}{24}\\ & = \frac{144 \pm \sqrt{144}}{24}\\ & = \frac{144 \pm 12}{24}. \end{align*}\]So we again get \(x_1 = 6.5\) and \(x_2 = 5.5\).
Now by using the perimeter equation above, we find
\[\begin{align*} x_1 = 6.5, \quad \rightarrow \quad y_1 &= 24 - 3 \times 6.5 \\ &= 4.5 \\ x_2 = 5.5, \quad \rightarrow \quad y_2 &= 24 - 3 \times 5.5 \\ &= 7.5. \end{align*}\]Thus there are two solutions, namely \(x_1 = 6.5\) yd., \(y_1 = 4.5\) yd. and \(x_2 = 5.5\) yd., \(y_2 = 7.5\) yd.
How ‘likely’ is this, that we find two viable solutions for \((x,y)\) here?
If we sketch the graphs of \(3x^2 + y^2 = 147\) (an ellipse) and \(3x + y = 24\) (a straight line), we are asking the line to cut the ellipse in two places, both in the first quadrant.
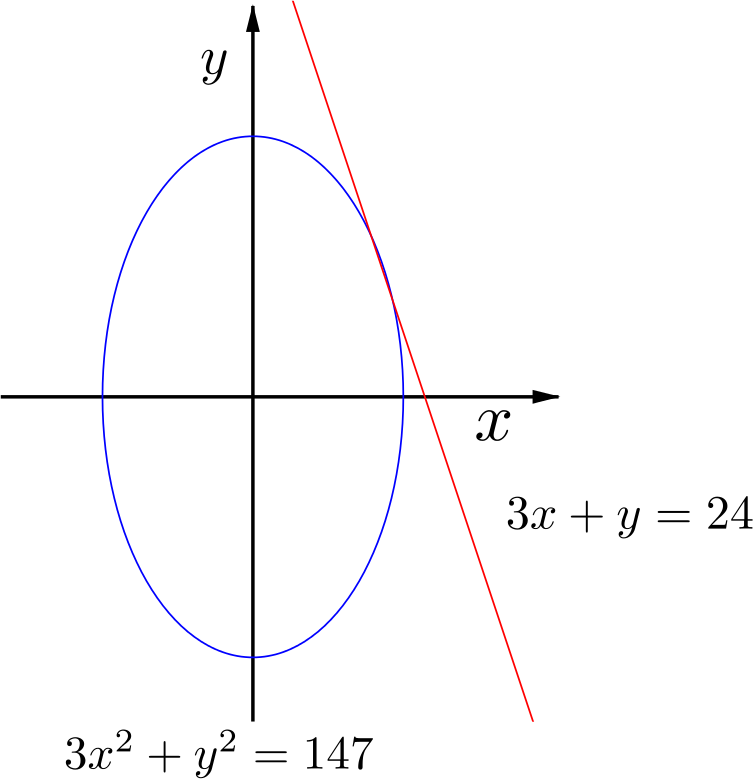
If the perimeter was \(100\) yd. instead of \(96\) yd. do we still get two solutions?

