Find the dimensions of the rectangle whose perimeter is \(\quantity{36}{m}\) and which is such that the square of the length of the diagonal is \(\quantity{170}{m^2}\).
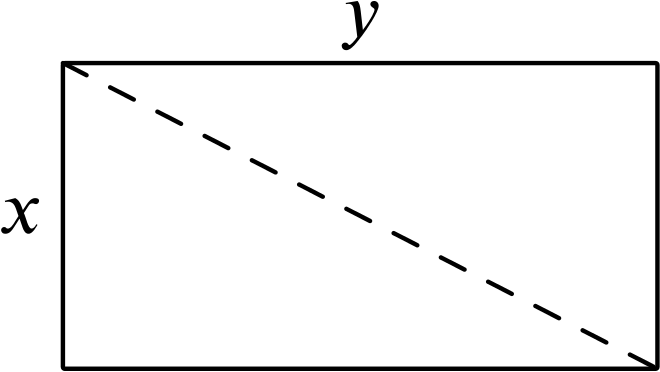
and that the square of the length of the diagonal is \(\quantity{170}{m^2}\), and so
\[\begin{equation}\label{eq:diag} x^2+y^2=170, \end{equation}\]by Pythagoras’ theorem.
Rearranging equation \(\eqref{eq:per}\), we find that \(y=18-x\), and so equation \(\eqref{eq:diag}\) becomes \[x^2+(18-x)^2=170,\] which when we multiply out the brackets becomes \[x^2+324-36x+x^2=170,\] and so the quadratic we must solve is \[2x^2-36x+154=0.\] We can divide this equation through by two and solve \[x^2-18x+77=0.\] We can factorise the equation \[(x-7)(x-11)=0.\] If \(x=7\), we must have \(y=11\), and \(x=11\) gives us that \(y = 7\).
Therefore the dimensions of the rectangle are \(\quantity{7}{m}\) by \(\quantity{11}{m}\).
This applet might help you visualise how the square on the diagonal varies with \(x\).
The red rectangle has perimeter \(36\).
When does the area of the square have its minimum value?
Notice how the two solutions for \(x\) and \(y\) are symmetrical.

