Which is bigger, \(\frac{2}{5}\) or \(\frac{1}{3}\)?
You could answer this question in several ways. We know about equivalent fractions, decimals and percentages so the question could be tackled by converting the fractions into decimals or percentages that are easily compared.
\(\frac{2}{5}=0.4\) or \(40\)% and \(\frac{1}{3}=0.333...\) or \(33.33...\)%. So \(\frac{2}{5}\) is bigger.
Alternatively, we can compare the two values as fractions. \(\frac{1}{3}\) is equivalent to \(\frac{2}{6}\). A sixth is smaller than a fifth so \(\frac{2}{5}\) is bigger.
Finding a common denominator gives us \(\frac{2}{5}=\frac{6}{15}\) and \(\frac{1}{3}=\frac{5}{15}\). So \(\frac{2}{5}\) is bigger.
Or, cross-multiplying the fractions gives \(2\times3>1\times5\). So \(\frac{2}{5}\) is bigger.
What if you had the fractions \(\frac{2x}{5}\) and \(\frac{x}{3}\)? Would your answer be the same?
Again, we can tackle this question in several ways. The important thing to notice here is that we now have a variable \(x\) in both fractions so our conclusion may well depend on the value of \(x\). If \(x=1\) then we have the original pair of fractions and so \(\frac{2x}{5}\) is bigger than \(\frac{x}{3}\). If \(x=0\) then both fractions equal 0 so neither is bigger.
We now need to consider other values of \(x\). Using the common denominator approach from above we know that the two fractions can be written as \(\frac{6x}{15}\) and \(\frac{5x}{15}\). When is \(6x>5x\)? Subtracting \(5x\) gives \(x>0\) so \(\frac{2x}{5}\) is bigger when \(x\) is positive. When \(x<0\) the fraction \(\frac{x}{3}\) is bigger.
We could have taken a different approach to this problem. We can represent both fractions graphically.
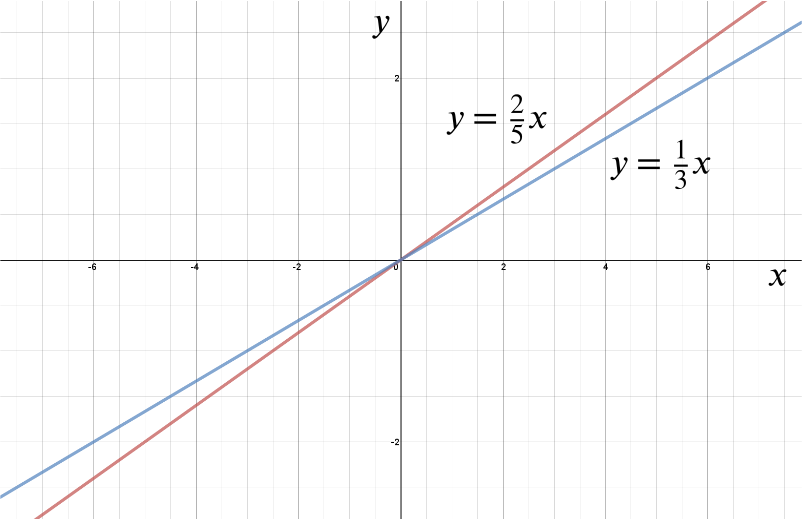
From this representation we can immediately see that for values of \(x\) less than zero, \(\frac{x}{3}\) will be bigger. For \(x=0\) the two fractions are equal and for \(x>0\), \(\frac{2x}{5}\) will be bigger.

