In the main problem you arranged four functions in a \(2 \times 2\) square according to two properties that the functions did or did not have. Now we will think about arranging eight functions in a \(2 \times 2 \times 2\) ‘cube’ based on whether or not the functions have three properties.
For example, can you complete this function cube for the following properties?
- Where the function is well defined, two different input values give two different output values
- The graph of function has asymptotes
- The graph of function has rotational symmetry about \((0,0)\)
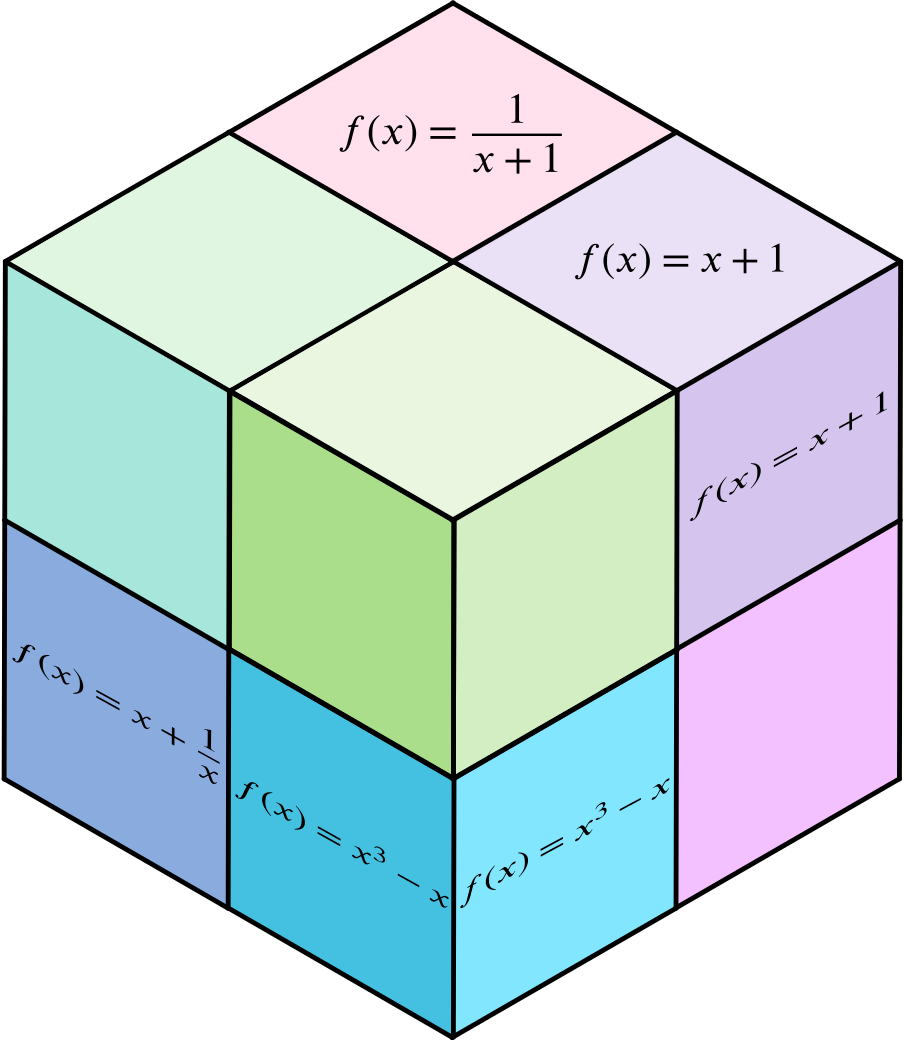
There are many ways to represent a cube and if you wanted to use the functions cards, you might find it simpler to arrange them in a \(4 \times 2\) table, i.e. two ‘layers’ of four functions.
For example, the table below could represent a function cube for the properties
- The graph passes through \((0,0)\)
- The graph is straight
- The \(y\)-axis is a line of symmetry for the graph
|
Graph passes through \((0,0)\) Graph is straight \(y\)-axis is a line of symmetry \[f(x)= \cdots\] |
Graph passes through \((0,0)\) |
|
Graph passes through \((0,0)\) |
Graph passes through \((0,0)\) |
|
Graph does not pass through \((0,0)\) |
Graph does not pass through \((0,0)\) |
|
Graph does not pass through \((0,0)\) |
Graph does not pass through \((0,0)\) |
Try to complete this function cube or make a different one.
You might need to make some extra function cards.
Make a note of any cells that you can’t think of functions for.
Make a note of properties that are difficult to combine in a function cube.

