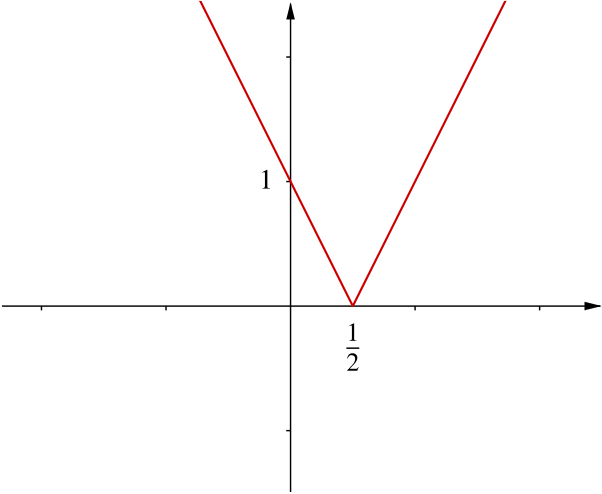
Sketch the graph of \(y=\big|2x-1\big|\).
We have that:
\[\big|2x-1\big|=\begin{cases} 2x-1 & \text{for } x \ge \dfrac{1}{2} \\ 1-2x & \text{for } x < \dfrac{1}{2} \\ \end{cases}\]
So the graph is composed of two straight lines of gradients \(2\) and \(-2\), meeting on the \(x\)-axis at \(\left(\dfrac{1}{2},0\right)\).
Determine the set of values of \(x\) for which \[\big|2x-1\big|>\frac{1}{x}.\]
We’ll use a combination of graph sketching and algebra; graph sketching allows us to see roughly where the inequality is satisfied, and we’ll then use algebra to find the exact values of the intersection point(s).
The inequality is satisfied whenever the graph of \(y=\big|2x-1\big|\) lies above the graph of \(y=\dfrac{1}{x}\).
The diagram below shows sketches of both \(y=\dfrac{1}{x}\) (in blue) and \(y=\big|2x-1\big|\) (in red), and the regions where \(y=\big|2x-1\big|\) lies above \(y=\dfrac{1}{x}\) are highlighted.
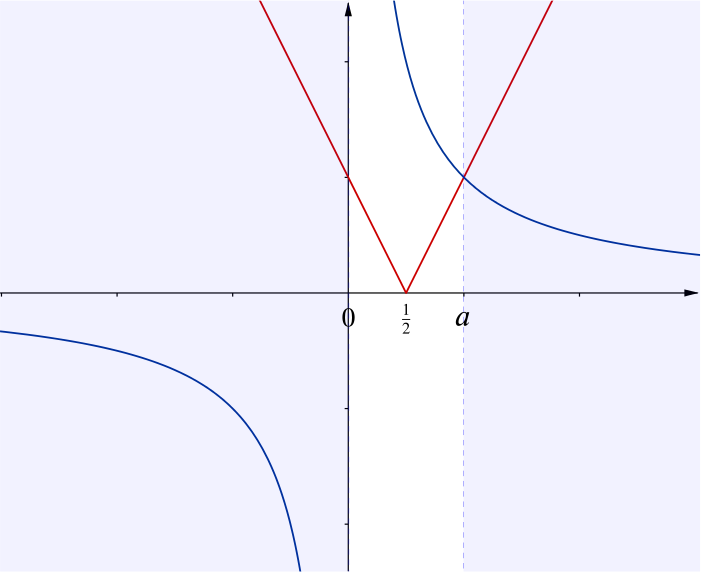
All points in the shaded regions have \(x\)-coordinates which satisfy \(x<0\) or \(x > a\). Here \(a\) is the \(x\)-coordinate of the point of intersection, so we know it is a solution to \(2x-1=\dfrac{1}{x}\).
Multiplying this through by \(x\), we derive the quadratic equation \(2x^2-x-1=0\). This factorises to \((2x+1)(x-1)=0\), so the solutions are \(x=-\dfrac{1}{2}\) and \(x=1\).
From the diagram we see that \(a\) is positive, so \(a=1\). Hence the inequality holds when \(x< 0\) or \(x>1\).
To which point in the diagram does the solution \(x=-\dfrac{1}{2}\) correspond?
How do we know that the graph doesn’t look like this?
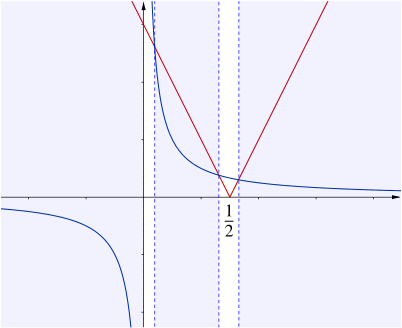
One way to see that it’s impossible for the graphs to intersect in the region \(0 < x < \dfrac{1}{2}\) is that in this region \(\dfrac{1}{x} > 2\) and \(1-2x < 1\).

