Find the set of real values of \(x\) for which \[\big |x+3\big |>2\big |x-3\big |.\]
The values of \(x\) for which the inequality is satisfied are the values of \(x\) for which the graph of \(\big |x+3\big |\) lies above the graph of \(2\big |x-3\big |\), so it is first helpful to sketch the graphs of \(y=\big |x+3\big |\) and \(y=2\big |x-3\big |\) on the same axes:
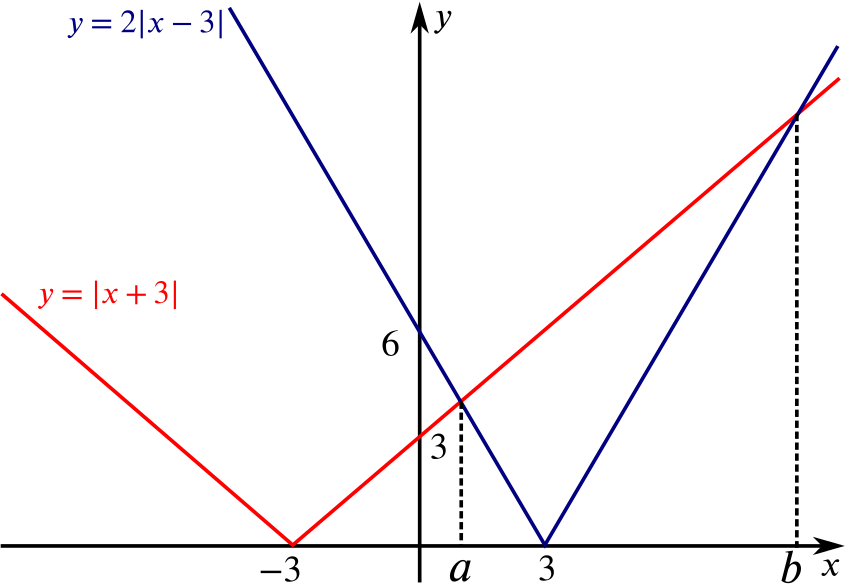
From this sketch, we see that the region where the inequality is satisfied will be of the form \(a < x < b\).
We see that \(a\) is the \(x\)-coordinate of the intersection of the lines \(y=x+3\) and \(y=-2(x-3)\), so \(a\) is the solution to \(x+3=-2x+6\), which gives \(a=1\).
The value \(b\) is the x-coordinate of the intersection of the lines \(y=x+3\) and \(y=2(x-3)\), so it is the solution of \(x+3=2x-6\), which gives \(b=9\).
Therefore the region where the inequality is satisfied is \(1<x<9\).

