Triangles come in many flavours. There are equilateral triangles (all three sides have equal length), scalene triangles (none of the sides have equal length), isosceles triangles (at least two sides have equal length), right-angled triangles, obtuse triangles (one angle is greater than \(90\) degrees), and acute triangles (all angles are less than \(90\) degrees). But all triangles have one thing in common (apart from having three sides): they are stable.
The best way to understand this is to think of a different shape, for example a square. If you make a square from four metal rods with hinges at their corners, you will find that it doesn’t stay square. It can easily be transformed into a parallelogram. You don’t have to bend the sides to do that, it happens just because of the hinges at the corners.
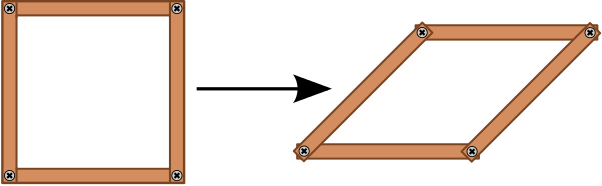
For a triangle, no matter what type, this can’t happen. It’s inherently rigid. That’s a very special property to have: all other polygons (shapes made out of straight line pieces connected at the end to form a circuit) are not rigid. This is why you see triangles all over the place in the world around you. In electricity pylons, cranes, bridges, and many houses.
Three-dimensional space is a little more permissive. Suppose you form a polyhedron by hinging together rigid faces at their edges. In the 19th century the French mathematician Augustin Louis Cauchy showed that all convex polyhedra are rigid. Convex means that any line connecting two points that are part of the polyhedron is also contained in the polyhedron. This means that the five familiar Platonic solids are rigid.
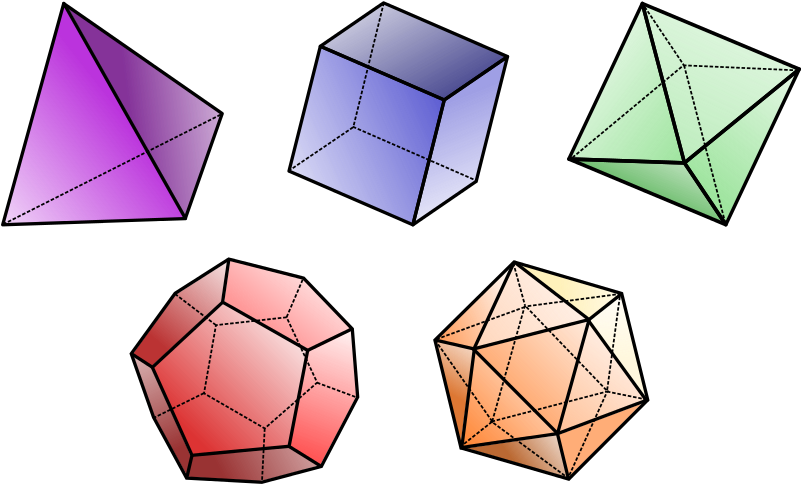
What can be said about non-convex polyhedra? The diagram below shows an icosahedron on the left, a convex polyhedron with twenty faces, contrasted with a solid known as a small stellated dodecahedron on the right. This is not convex as, for example, the lines between two of the pointed vertices are not always contained in the polyhedron.
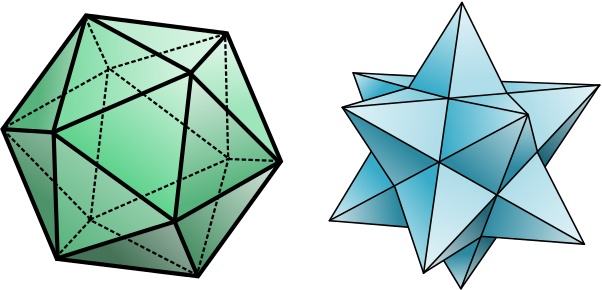
It turns out that the small stellated dodecahedron is rigid, but for a very long time nobody was able to prove whether that’s true for all non-convex polyhedra. Then, in 1977, the mathematician Robert Connelly found one that isn’t. It has eighteen triangular faces, but later a simpler example was found by Klaus Steffen with only fourteen triangular faces and nine vertices.
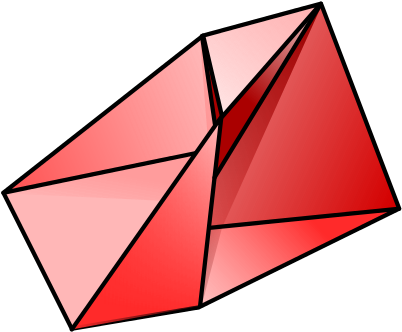
You might like to make your own flexible polyhedron, so here is a net. There is also a pdf version that you may find convenient for printing.