We define the digit sum of a non-negative integer to be the sum of its digits. For example, the digit sum of \(123\) is \(1+2+3=6\).
- How many positive integers less than \(100\) have digit sum equal to \(8\)?
It helps to write all positive integers less than \(100\) as two-digit numbers, where the first digit could be \(0\).
These are \(9\) such integers: \(08, 17, 26, 35, 44, 53, 62, 71, 80\).
Let \(n\) be a positive integer with \(n<10\).
- How many positive integers less than \(100\) have digit sum equal to \(n\)?
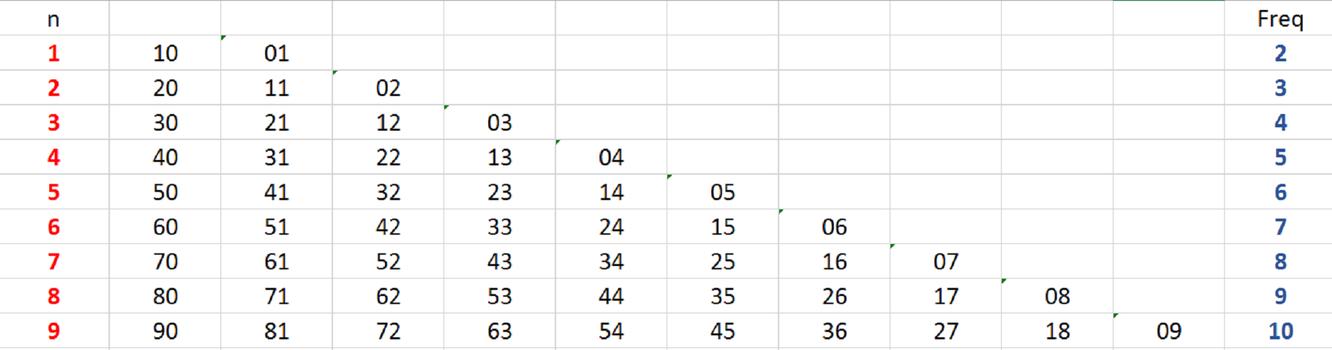
When \(n=1\), we have \(2\) such numbers: \(01, 10\). When \(n=2\), we have \(3\) such numbers: \(02, 11, 20\). When \(n=3\), we have \(4\) such numbers: \(03, 12, 21, 30\). And so on…
We can see that every time \(n\) increases by \(1\), the number of positive integers with digit sum equal to \(n\) also increases by \(1\).
So there are \(n+1\) such integers.
- How many positive integers less than \(1000\) have digit sum equal to \(n\)?
Let’s try to answer this question for \(n = 8\) again.
What will the end digit of our number with digit-sum \(8\) be?
If it’s \(0\), then the possibilities are \(800, 710, ..., 080\). There are \(9\) such numbers.
If the final digit is \(1\), then we have \(701, 611,..., 071\). There are \(8\) such numbers.
If the final digit is \(2\), there are \(7\) such numbers.
And so on… until we have the final digit as \(8\), when we have \(008\). There is \(1\) such number.
Thus for \(n = 8\), there are \(0.5 \times 9 \times 10 = 45\) such numbers in total.
It is easy to generalise this argument, to show that in the general case, there are \(\dfrac{(n+1)(n+2)}{2}\) such numbers.
- How many positive integers between \(500\) and \(999\) have digit sum equal to \(8\)?
What can the first two digits be? Our table shows us there are ten possible numbers that could gives us these.
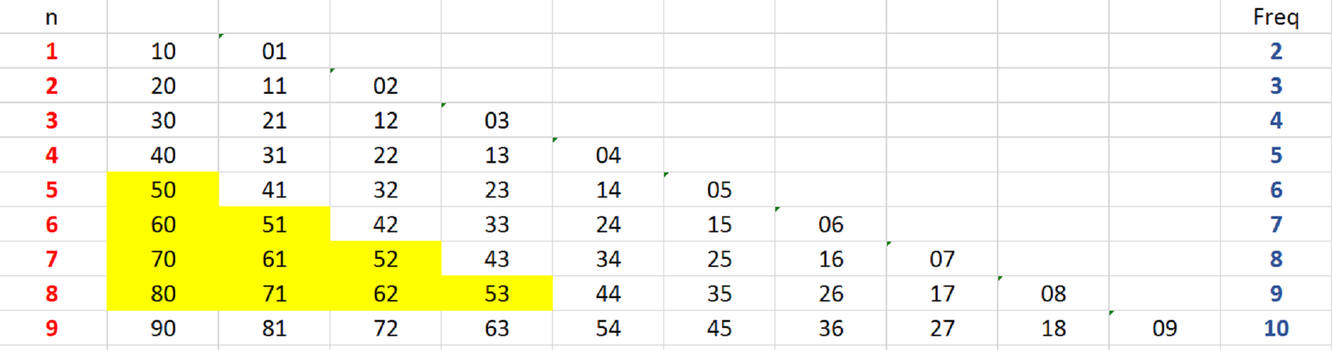
Given the first two digits, we know the last. Thus the answer is \(10\).
- How many positive integers less than \(1000\) have digit sum equal to \(8\), and one digit at least \(5\)?
We can now write all our numbers as three-digit numbers, where one or both of the first two digits could be \(0\).
From part (iv), we have that there are \(10\) possibilities in the case that the hundreds digit is at least \(5\).
By symmetry, there are also \(10\) numbers when the tens digit is at least \(5\), and another \(10\) when the units digit is at least \(5\).
These sets are disjoint (have no elements in common), so there are \(30\) such integers altogether.
Alternatively, we can draw up a further table. We know one digit is 5, 6, 7 or 8, and we know we are adding two extra digits to this (that may be 0).
The possibilities for these extra digits are very limited, and it is easy to write down explicitly the possible numbers.
- What is the total of the digit sums of the integers from \(0\) to \(999\) inclusive?
Each digit from \(0\) to \(9\) appears \(100\) times in the hundreds position.
Each digit from \(0\) to \(9\) appears \(10\) times \(10\) times in the tens position.
Each digit from \(0\) to \(9\) appears singly \(100\) times in the units position.
That makes \(300\) times altogether for each digit.
Therefore the total of the digit sums is
\[300 \times (0+1+2+3+4+5+6+7+8+9)= 13500.\]

