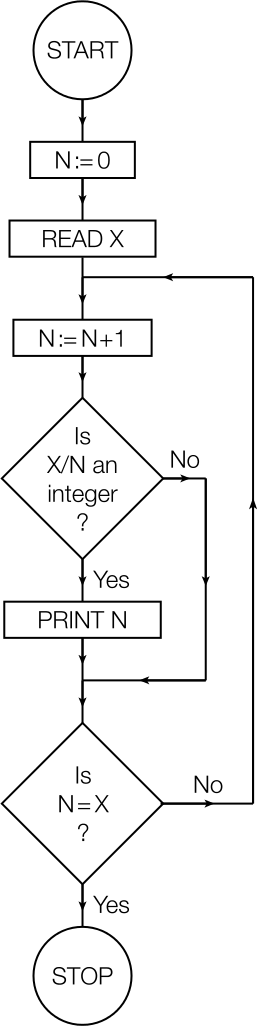
State what numbers will be printed from this flow chart if \(X\) is read as (a) \(6\),
We begin with \(X = 6\).
| \(N\) | \(X/N\) | Integer? | \(N=X\)? |
|---|---|---|---|
| \(1\) | \(6\) | Yes | No |
| \(2\) | \(3\) | Yes | No |
| \(3\) | \(2\) | Yes | No |
| \(4\) | \(\dfrac{3}{2}\) | No | No |
| \(5\) | \(\dfrac{5}{2}\) | No | No |
| \(6\) | \(1\) | Yes | Yes |
Thus, the flow chart prints out the values \(1\), \(2\), \(3\), and \(6\).
(b) \(9\)
We next take \(X = 9\). Again, we can build a table like the above; the only values of \(N\) for which \(X/N\) is an integer are \(1\), \(3\), and \(9\), and so these are the values printed.
and (c) \(20\)
Finally, we take \(X = 20\). As above, the only values of \(N\) for which \(X/N\) is an integer are \(1\), \(2\), \(4\), \(5\), \(10\), and \(20\); these are the values of \(N\) that are printed.
What is the relation between \(X\) and the numbers printed?
The numbers printed are the positive integers (including \(X\)) that divide \(X\) exactly.
This flow chart is intended for use with \(X\) being a positive integer. What would happen if \(X\) were read to be \(2.4\)? Suggest a simple change to the second decision box to avoid this problem.
If \(X\) were to be \(2.4\), the flow chart would loop endlessly, since at no point will it be true that \(N = X\).
In place of the question ‘\(N=X\)?’, we could instead ask the question ‘\(N > X\)?’

