The Millennium school has \(1000\) students and \(1000\) student lockers. The lockers are in line in a long corridor and are numbered from \(1\) to \(1000\).
Initially all the lockers are closed (but unlocked).
The first student walks along the corridor and opens every locker.
The second student then walks along the corridor and closes every second locker, i.e. closes lockers \(2,4,6,\) etc. At that point there are \(500\) lockers that are open and \(500\) that are closed.
The third student then walks along the corridor, changing the state of every third locker.Thus s/he closes locker \(3\) (which had been left open by the first student), opens locker \(6\) (closed by the second student), closes locker \(9\), etc.
All the remaining students now walk in order, with the \(k\)th student changing the state of every \(k\)th locker, and this continues until all \(1000\) students have walked along the corridor.
It’s a help to write down the first few passes for low-numbered lockers.

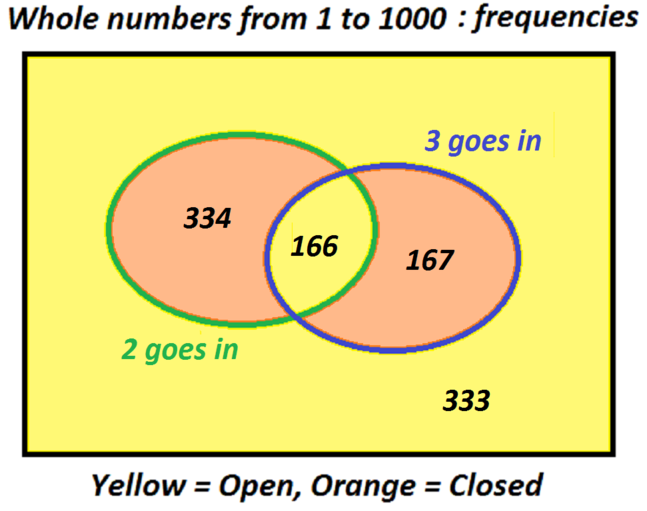
- How many lockers are closed immediately after the third student has walked along the corridor? Explain your reasoning.
The pattern of openness repeats every \(6\) (= lowest common multiple of \(1,2\) and \(3\)) lockers. The first six lockers are in the state \(011100\) after the third student has passed.
Now \(1000 = 6 \times 166 + 4\), so \(166 \times 3 + 3 = 501\) lockers are closed and \(499\) are open.
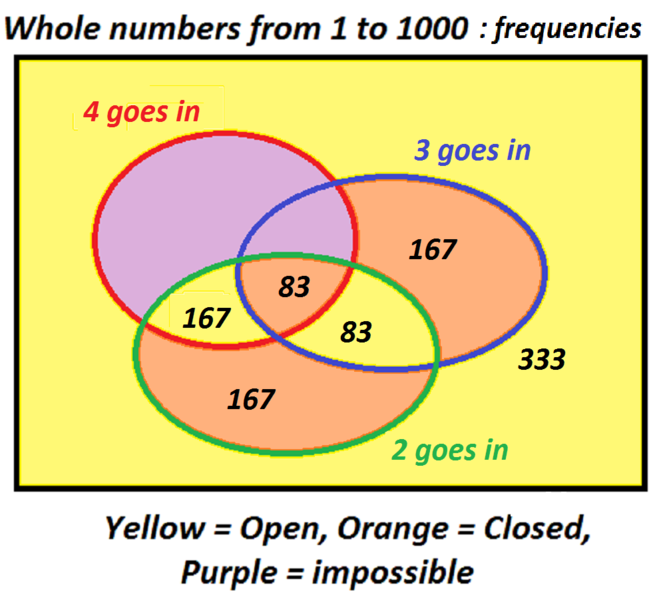
- How many lockers are closed immediately after the fourth student has walked along the corridor? Explain your reasoning.
The pattern of openness repeats every \(12\) (= lowest common multiple of $1,2,3 $ and \(4\)) lockers now. The first twelve lockers are in the state \(011000001101\) after the fourth student has passed.
Now \(1000 = 12 \times 83 + 4\), so the number of closed lockers is \(5 \times 83 + 2\) which is \(417\).
- At the end (after all \(1000\) students have passed), what is the state of locker \(100\)? Explain your reasoning.
The state of locker \(n\) after all the passes depends on the number of divisors \(n\) has (this number is called \(d(n)\)).
As the students 1 to \(n\) make their pass, the state of the locker changes \(d(n)\) times.
It is easy to check that \(d(100) = 9\).
Therefore, after all students have passed, locker \(100\) is open, since it’s closed to start with.
- After the hundredth student has walked along the corridor, what is the state of locker \(1000\)? Explain your reasoning.
This time we need to ask, how many factors less than or equal to \(100\) does \(1000\) have?
This is \(d(100) = 9\), since anything dividing into \(100\) goes into \(1000\).
So the \(1000\)th locker is open after the \(100\)th pass.
It’s worth noting that if \(n\) has a factor \(m\), this can usually be paired with \(\dfrac{n}{m}\), another factor of \(n\), and so \(d(n)\) is even.
The only time this argument breaks down is if \(n = s^2\) is a perfect square. Now \(\dfrac{n}{s}=s\), and we cannot count \(s\) twice as a factor.
So this means that after the \(1000\)th pass, the only lockers open will be \(1,4,9,16,..., 961\).
The \(1000\)th locker will be closed, as \(1000\) is not a square.

