where \(R\) is the radius of the circumcircle of the triangle \(ABC\).
[You need consider only the case when the angle \(A\) is acute.]
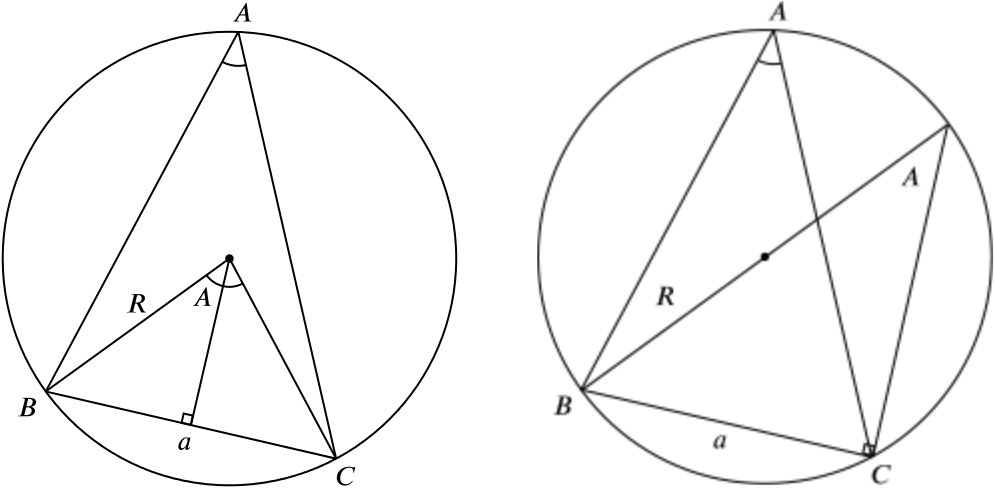
In the diagram on the left we have used the facts that
- the perpendicular from the centre bisects the chord \(BC\), and
- the angle at the centre is twice the angle at the circumference.
Now we can see that \(R \sin A = \dfrac{a}{2}\). Alternatively, in the diagram on the right we have used the facts that
- the angles subtended at the circumference are equal, and
- the angle in a semi-circle is a right-angle.
This shows us that \(\sin A = \dfrac{a}{2R}\).
Either of these gives us \(\dfrac{a}{\sin A} = 2R\) as required.
Hence or otherwise deduce that
- \(a \cos A + b \cos B = c \cos (A-B)\),
We will use the identities \(\sin 2x = 2\sin x \cos x\), \(\sin (\pi - x) = \sin x\), and \(\sin x + \sin y = 2\sin \dfrac{x+y}{2}\cos \dfrac{x-y}{2}\).
as required.
- \(a \cos A + b \cos B + c \cos C = 4 R \sin A \sin B \sin C\).
We’ll use the additional identities \(\cos x + \cos y = 2\cos\dfrac{x+y}{2}\cos\dfrac{x-y}{2}\), and \(\cos\left(\dfrac{\pi}{2}-x\right) = \sin x\).

