- Prove the identity \[\cos \theta - 2 \cos 3 \theta + \cos 5\theta = 2\sin \theta (\sin 2 \theta - \sin 4 \theta).\]
We can always write the expressions \(\cos A + \cos B, \cos A - \cos B, \sin A + \sin B\), and \(\sin A - \sin B\) as the product of two \(\sin / \cos\) terms.
This can be immensely useful to us in lots of situations. Here we are interested in \(\cos A - \cos B\).
We begin with \[\cos(X + Y) = \cos X \cos Y - \sin X \sin Y \quad \text{and} \quad \cos(X - Y) = \cos X \cos Y + \sin X \sin Y.\] Adding these equations gives \[\cos (X-Y) - \cos (X+Y) = 2\sin X \sin Y.\] Now setting \(A=X-Y, B=X+Y\) we find \[\cos A - \cos B = 2 \sin \frac{A+B}2 \sin \frac{B-A}2.\]
Applying this to both \(\cos\theta - \cos 3\theta\) and \(\cos 5 \theta - \cos 3\theta\), we see the left-hand side (LHS) is equal to \[2 \sin 2\theta \sin \theta + 2 \sin 4\theta \sin (-2\theta) = 2 \sin \theta(\sin 2\theta - \sin 4 \theta),\] as required.
Alternatively, we can show by expanding that if \(c = \cos\theta, s = \sin\theta\), then \[\cos(3\theta) = 4c^3-3c, \quad \cos(5\theta) = 16c^5-20c^3+5c, \quad \sin(2\theta) = 2sc, \quad \sin(4\theta) = 8sc^3-4sc.\]
Now the LHS is \[c - 2(4c^3-3c)+ 16c^5-20c^3+5c=16c^5-28c^3+12c,\] while the RHS is \[2s(2sc-(8sc^3-4sc)) = 2(1-c^2)(-8c^3+6c) = 16c^5-28c^3+12c,\] which are the same, and so we are done.
Solve the equations
\(\cos 2x = \sin x\),
\(3 \sec^2 x = \tan x + 5\)
giving in each case all solutions between \(0^\circ\) and \(360^\circ\).
- For the first equation, we use one of the double angle formulae for \(\cos\), that’s \(\cos 2x = 1 - 2\sin^2 x\).
Now everything’s written in terms of \(\sin x\), which makes the equation much simpler.
Writing \(u=\sin x\), we have to solve the equation \(\cos 2x = \sin x,\) which gives \[1 - 2u^2 = u, \quad \text{ or} \quad 2u^2+u-1=0, \quad \text{ or} \quad (2u-1)(u+1)=0,\]
with solutions \[\sin x = u = \frac{1}{2}, -1.\]
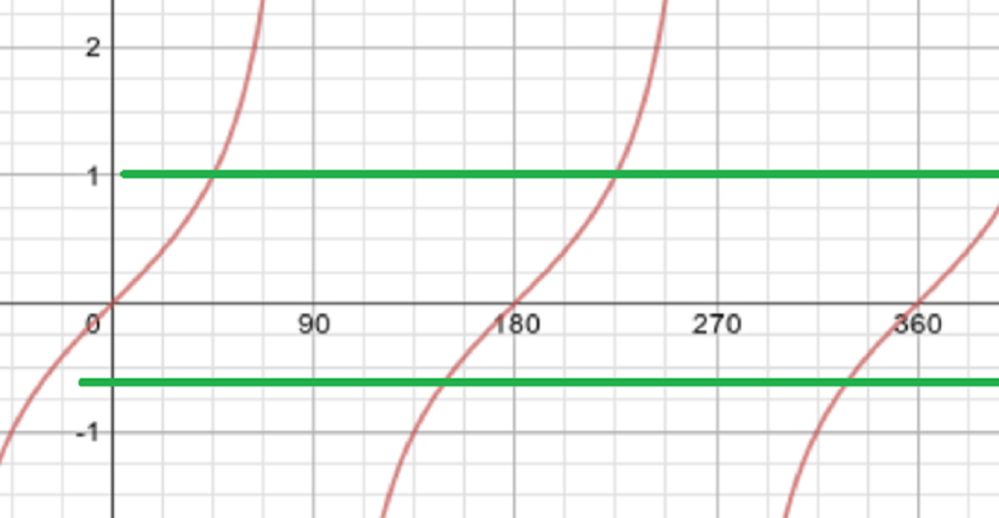
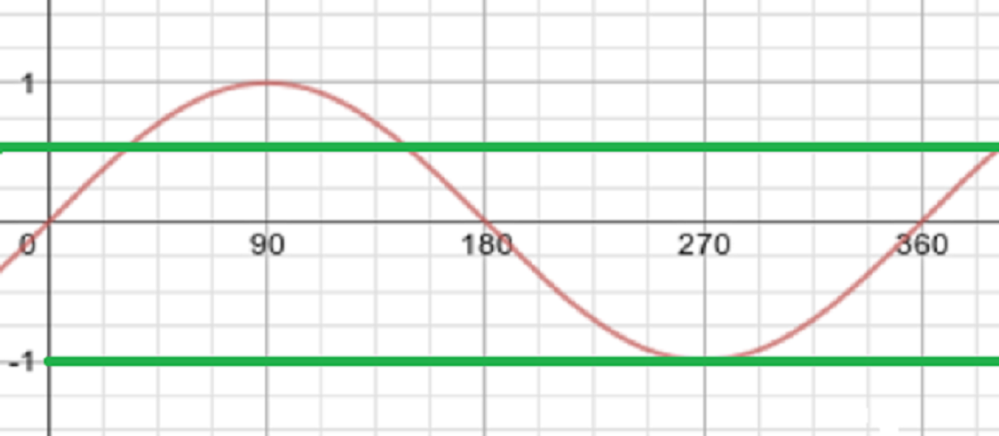
We need all solutions between \(0^\circ\) and \(360^\circ\). These are \[x = 30^\circ, 150^\circ, 270^\circ.\]
It’s helpful to sketch a graph, to check we’ve got all the solutions.
- For the second, recall the identity \(\tan^2 x + 1 = \sec^2 x\) (given by dividing \(\sin^2 x + \cos^2 x = 1\) by \(\cos^2 x\)).
Define \(v = \tan x\), so we need to solve
\[3 \sec^2 x = \tan x + 5, \quad \text{ or} \quad 3(1+v^2)-v-5=0, \quad \text{ or} \quad 3v^2 -v -2=0.\] This is \((3v+2)(v-1)=0\), so \(v = -\frac {2}{3}, 1\), which (since \(\tan x\) has period \(\pi\)) gives the four solutions \[x = 45^\circ, 225^\circ, 146.3^\circ, 326.3^\circ.\]