Using angles in a pentagon...

Add to your resource collection Remove from your resource collection Add notes to this resource View your notes for this resource

Method 1

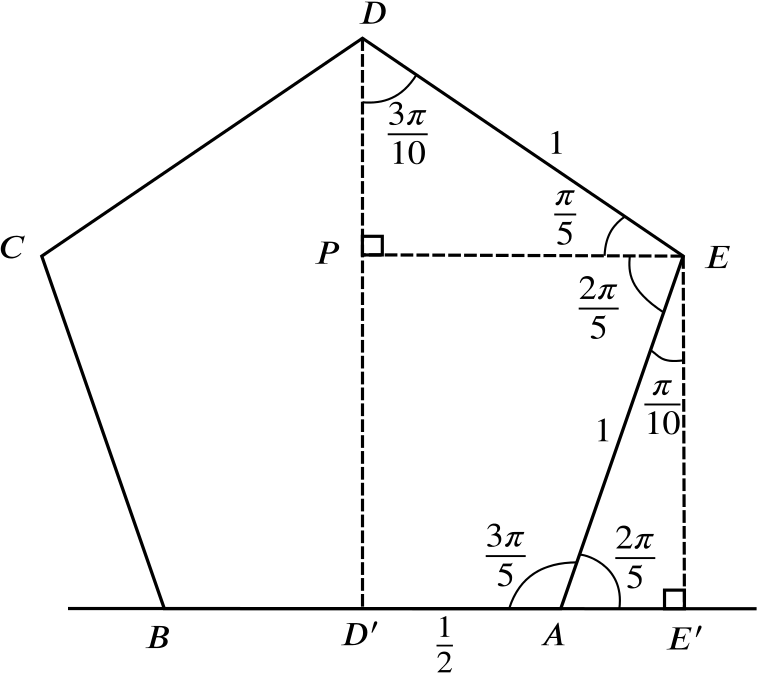
The sum of angles inside a \(n\)-sided polygon is \((n-2)\pi\), so each angle inside our regular pentagon is \(\dfrac{3\pi}{5}\). For simplicity we choose each side to be of length \(1\).

Let \(D'\) and \(E'\) be the points \(D\) and \(E\) projected onto the line \(AB\) as shown. Since \(ABCDE\) is a regular pentagon, \[D'A =\frac{1}{2}.\] From the right-angled triangle \(AEE'\) we see that \[AE' =\cos\frac{2\pi}{5},\] and from the triangle \(DPE\) we find that \[D'E' = PE =\cos\frac{\pi}{5}.\] Since \[D'E' = D'A + AE',\] we get the result \[\begin{equation*} \cos\frac{\pi}{5}-\cos\frac{2\pi}{5}=\frac{1}{2}. \qquad \label{eq:star}\tag{$*$} \end{equation*}\]

Method 2

The question says ‘or otherwise’, so we’re free to pick another method if we wish.

The regular pentagon is intimately connected with \(\phi\), the Golden Ratio \(= 1.61803...\), which is the positive solution to \(x^2 - x - 1 = 0\).

Using the Cosine Rule in \(ABD\) one way, \(\cos \dfrac{2\pi}{5} = \dfrac{1}{2\phi}\). Using the Cosine Rule in \(ABD\) another way, \(\cos \dfrac{\pi}{5} = \dfrac{2\phi^2-1}{2\phi^2}\).

Thus \[\cos\dfrac{\pi}{5}-\cos\dfrac{2\pi}{5} = \dfrac{2\phi^2-1}{2\phi^2}- \dfrac{1}{2\phi} = \dfrac{2\phi^2-1}{2\phi^2}- \dfrac{\phi}{2\phi^2}= \dfrac{2\phi^2-\phi-1}{2\phi^2} = \dfrac{\phi^2}{2\phi^2} = \dfrac{1}{2}.\]

Let \[\gamma=\cos\frac{\pi}{5}.\] Using the cosine double angle formula \[\cos 2\theta=2\cos^2\theta-1\] with \(\theta=\dfrac{\pi}{5},\) we can use \(\eqref{eq:star}\) to get \[\begin{align*} \gamma-(2\gamma^2-1) &= \frac{1}{2} \\ \iff \quad 4\gamma^2-2\gamma-1 &= 0. \end{align*}\]

We then use the quadratic formula to solve for \(\gamma\): we have \[\gamma = \cos\frac{\pi}{5}=\frac{2\pm\sqrt{4-4\times 4\times (-1)}}{2\times 4}=\frac{1\pm\sqrt{5}}{4}.\] We know that \(\dfrac{\pi}{5} < \dfrac{\pi}{2}\) so \(\cos\dfrac{\pi}{5}>0\) and thus we choose the positive root: \[\cos\frac{\pi}{5}=\frac{1+\sqrt{5}}{4}.\]

We use the fact that \[\cos(\pi-\theta)=-\cos\theta,\] which we can see from the diagram.

This gives \[\cos\frac{3\pi}{5}=-\cos\frac{2\pi}{5}\] so \[\begin{align*} \cos\frac{3\pi}{5} &= -\cos\frac{2\pi}{5}=\frac{1}{2}-\cos\frac{\pi}{5}\\ &= \frac{2-(\sqrt{5}+1)}{4}=-\frac{\sqrt{5}-1}{4} \end{align*}\]

as required.