An exact value for $\sin 15^{\circ}$...

Add to your resource collection Remove from your resource collection Add notes to this resource View your notes for this resource

We will use the identity \(\sin(x-y) = \sin x \cos y - \sin y \cos x\). We have that \[\begin{align*} \sin 15^\circ=\sin(45-30)^\circ &=\sin45^\circ\cos30^\circ-\cos45^\circ\sin30^\circ \\ &=\frac{1}{\sqrt{2}}\frac{\sqrt{3}}{2}-\frac{1}{\sqrt{2}}\frac{1}{2} \\ &=\frac{\sqrt{2}\sqrt{3}}{2\times 2}-\frac{\sqrt{2}}{2\times 2} \\ &=\frac{\sqrt{6}-\sqrt{2}}{4}. \end{align*}\] We now have \[\begin{align*} \cos^2 15^\circ=1-\sin^2 15^\circ &=1-\frac{6+2-2\sqrt{6}\sqrt{2}}{16} \\ &=\frac{8+2\sqrt{12}}{16}\\ &=\frac{6+2+2\sqrt{2}\sqrt{6}}{16} \\ &=\frac{(\sqrt{6}+\sqrt{2})^2}{4^2}, \end{align*}\]

and so, since \(\cos \theta\) is positive between \(0^\circ\) and \(90^\circ\), \[\cos 15^\circ=\frac{\sqrt{6}+\sqrt{2}}{4}.\]

Finally, we have \[\begin{align*} \tan 15^\circ=\frac{\sin15^\circ}{\cos15^\circ} &=\frac{\sqrt{6}-\sqrt{2}}{\sqrt{6}+\sqrt{2}} \\ &=\frac{(\sqrt{6}-\sqrt{2})^2}{(\sqrt{6}+\sqrt{2})(\sqrt{6}-\sqrt{2})} \\ &=\frac{6+2-2\sqrt{2}\sqrt{6}}{6-2} \\ &=\frac{8-2\sqrt{12}}{4} \\ &=2-\sqrt{3}. \end{align*}\]

First let’s draw what’s happening, filling in the angles by putting in \(a\) for \(ACB\) and \(b\) for \(CAE\).

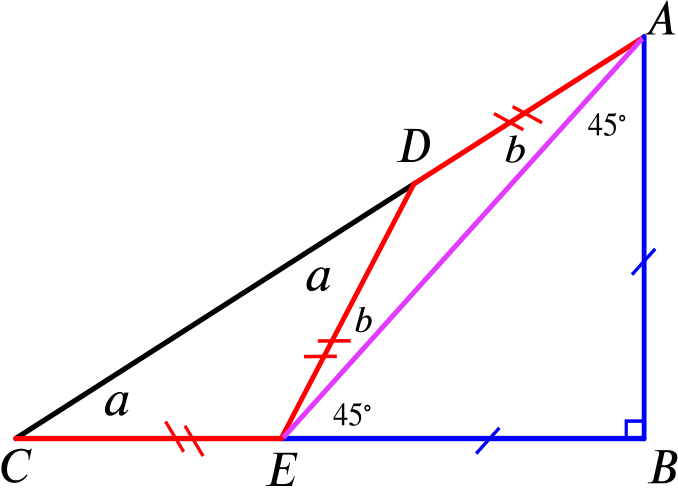
The angle-sum in triangle \(ABC\) tells us that \(a+b = 45^\circ\). The angle at \(D\) tells us that \(a = 2b\). Solving these equations simultaneously gives \(b = 15^\circ, a = 30^\circ\).

We need the ratio of \(DC\) to \(AB\). Without loss of generality we can put \(CE = 1\), so \(CD = 2 \cos 30^\circ\) and \(EA = 2\cos 15^\circ\).

Now, by Pythagoras, \(AB = \dfrac{2\cos 15^\circ}{\sqrt{2}}\).

Thus \[\begin{align*} DC:AB &= 2\cos 30^\circ: \dfrac{2\cos 15^\circ}{\sqrt{2}}\\ &= \sqrt{3} : \sqrt{2}\frac{\sqrt{6}+\sqrt{2}}{4} \\ &= 4\sqrt{3} : \sqrt{12}+2 \\ &=2\sqrt{3} : \sqrt{3}+1. \end{align*}\]