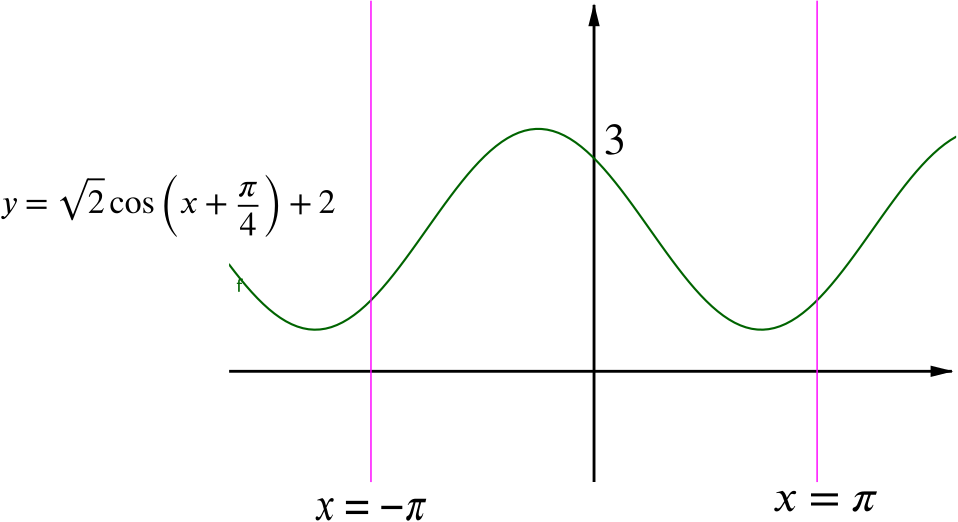
Give a sketch for \(-\pi \leq x \leq \pi\) of the curve \[y = \cos x - \sin x +2.\]
Firstly we can rewrite the right hand side using one of the compound angle identities, such as \[R\cos(x+\theta)=R\cos x\cos \theta- R\sin x \sin \theta.\]
If we put \(R\cos \theta = 1\) and \(R \sin \theta = 1\), where \(R > 0\) and \(\theta\) is acute, we have (on dividing these equations) \(\tan \theta = 1 \implies \theta = \dfrac{\pi}{4}\).
On squaring and adding these equations, we have \[R^2 = 2 \implies R = \sqrt{2}.\]
This gives us that \(\sqrt{2}\cos\left(x+\dfrac{\pi}{4}\right) = \cos x - \sin x\), so the curve we are asked to sketch is \[y = \sqrt{2}\cos\left(x+\dfrac{\pi}{4}\right) +2.\]
So this is our standard cosine curve, stretched in the \(y\)-direction by a scale factor of \(\sqrt{2}\), translated by \(\dfrac{\pi}{4}\) to the left, and upwards by \(2\).