When is $\sin\theta > \sin 3\theta$?

Add to your resource collection Remove from your resource collection Add notes to this resource View your notes for this resource

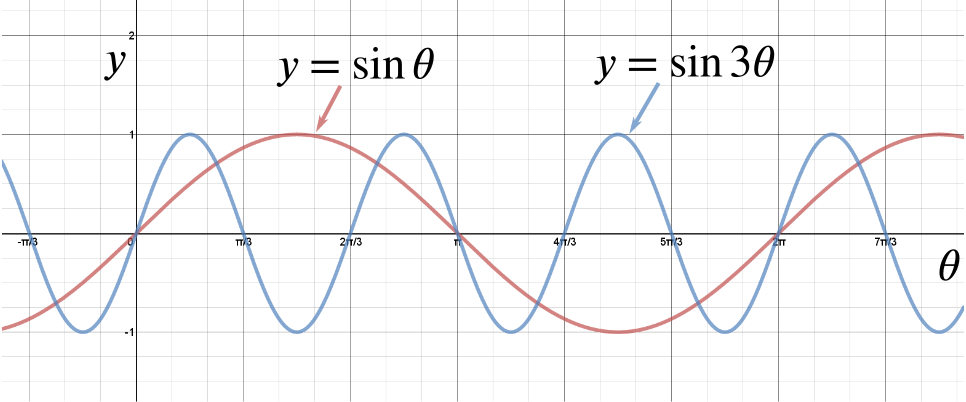
So we get intersections when \[\sin \theta=\sin 3 \theta.\]

Now \[\sin A= \sin B \iff A = B + 2n\pi \quad \text{OR} \quad A= \pi - B + 2n\pi,\] where \(n\) is a whole number.

So here we have \[\theta = 3\theta + 2n\pi \implies \theta = -n\pi \quad \text{OR} \quad \theta = \pi - 3\theta + 2n\pi \implies \theta = \dfrac{(2n+1)\pi}{4}.\]

So the intersection points for \(y = \sin \theta\) and \(y = \sin (3\theta)\) in the given range are \(0, \dfrac{\pi}{4},\dfrac{3\pi}{4},\pi,\dfrac{5\pi}{4},\dfrac{7\pi}{4}, 2\pi.\)

Now looking back at our sketch, we can pinpoint the ranges where \(\sin\theta > \sin 3 \theta\) as \[\begin{align*} \frac{\pi}{4} &< \theta < \frac{3\pi}{4} \\ \pi &< \theta < \frac{5\pi}{4} \\ \frac{7\pi}{4} &< \theta < 2\pi. \end{align*}\]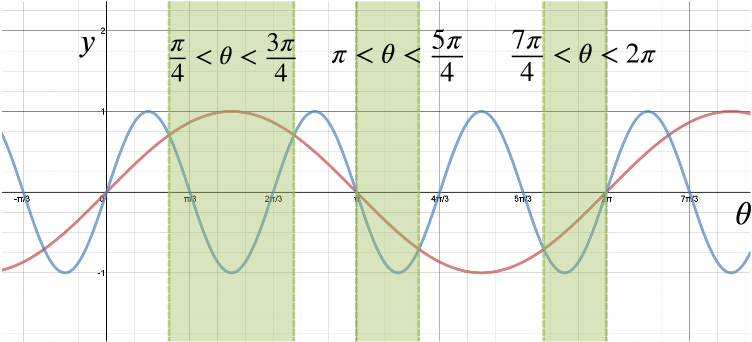

Alternatively, we could say

\[\sin 3 \theta = \sin (\theta + 2\theta)=\sin\theta\cos (2\theta) +\sin (2 \theta) \cos \theta.\] That is, we have the equation \[\begin{align*} \sin \theta &= \sin\theta(1-2\sin^2 \theta) +2\sin \theta \cos^2 \theta \\ &= \sin \theta - 2\sin^3\theta + 2\sin\theta(1-\sin^2 \theta)\\ &= 3\sin\theta - 4\sin^3\theta. \end{align*}\]

Thus we want to solve \[\sin \theta (2\sin^2 \theta -1) =0.\] The first part of the equation, \(\sin\theta = 0\), gives the solutions \(\theta = 0,\pi,2\pi\).

The second part of the equation, \(2\sin^2 \theta -1 =0\), can be rearranged to \(\sin\theta = \pm \dfrac{1}{\sqrt{2}}\), and so gives the solutions \(\theta = \dfrac{\pi}{4},\,\dfrac{3\pi}{4},\,\dfrac{5\pi}{4},\,\dfrac{7\pi}{4}\) in this range.