Given that \(\sin \alpha = \dfrac{3}{5}\) and \(\cos \beta = \dfrac{12}{13}\), prove that one possible value of \(\cos(\alpha + \beta)\) is \(\tfrac{33}{65}\) and find all the other possible values.
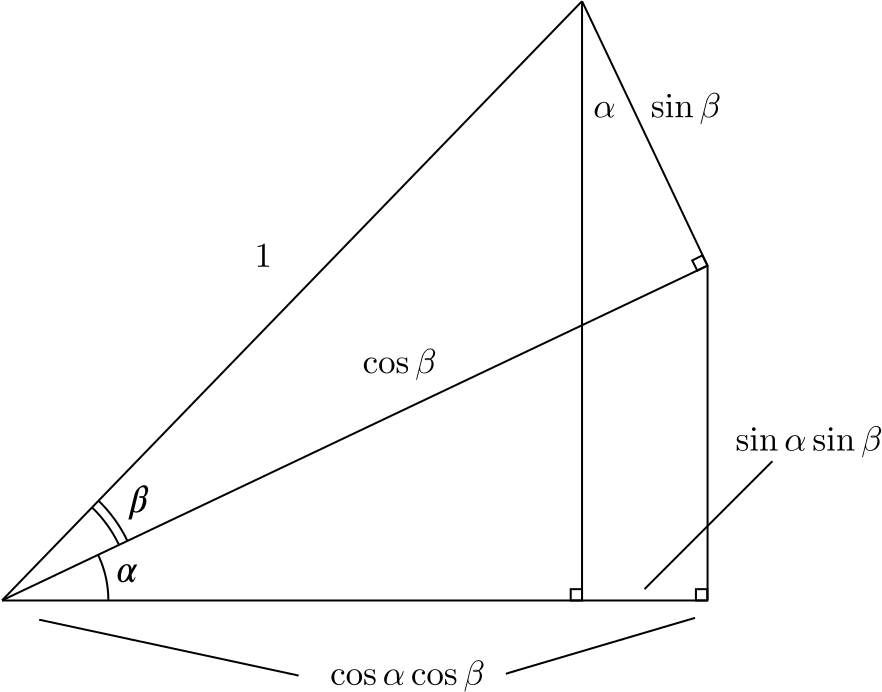
The diagram tells us that \(\cos(\alpha+\beta) = \cos\alpha\cos\beta-\sin\alpha\sin\beta\) for \(\alpha+\beta < 90^\circ\). This is, in fact, true for all angles \(\alpha\) and \(\beta\).
Now \(\cos^2 \theta + \sin^2 \theta = 1\) for all \(\theta\), which means \(\cos \alpha = \pm\dfrac{4}{5}\), and \(\sin \beta = \pm \dfrac{5}{13}\).
Thus \(\cos(\alpha+\beta) = \cos\alpha\cos\beta-\sin\alpha\sin\beta = \pm \dfrac{48}{65}\pm \dfrac{15}{65},\) where the signs are independent of each other.
We therefore have four solutions, \(\cos(\alpha+\beta) = \pm \dfrac{63}{65}\), or \(\pm \dfrac{33}{65}\).

