Points \(A\) and \(B\) have position vectors \(\mathbf{a}\) and \(\mathbf{b}\) respectively relative to a point \(O\). Given that \(L\) is the midpoint of \(OA\), and that \(M\) is the point on \(OB\) produced such that \(OM = 3OB\), express \(\overrightarrow{LM}\) in terms of \(\mathbf{a}\) and \(\mathbf{b}\).
Given further that \(P\) is the point on \(LM\) such that \(LP = \lambda LM\), express \(\overrightarrow{AP}\) in terms of \(\mathbf{a, b}\) and \(\lambda\).

We have that \(\overrightarrow{OM} = 3\mathbf{b}, \overrightarrow{OL} = \dfrac{1}{2}\mathbf{a}\), so \(\overrightarrow{LM}= 3\mathbf{b}- \dfrac{1}{2}\mathbf{a}.\)
The vector \[\begin{align*} \overrightarrow{AP} &= \overrightarrow{OP} - \overrightarrow{OA} \\ &= (\overrightarrow{OL}+\lambda \overrightarrow{LM}) - \mathbf{a} \\ &= \dfrac{1}{2}\mathbf{a}+\lambda\left( 3\mathbf{b}- \dfrac{1}{2}\mathbf{a}\right) -\mathbf{a}\\ &=3\lambda \mathbf{b} - \dfrac{1}{2}\mathbf{a}(1+\lambda). \end{align*}\]In the case where \(A, P\) and \(B\) are collinear, calculate the value of
- \(\lambda\)
- \(\dfrac{AP}{PB}\).
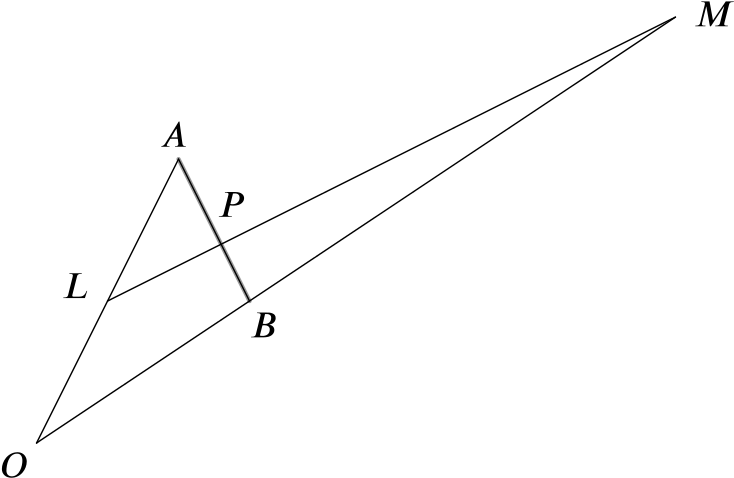
If \(P\) is on \(AB\), then \(\overrightarrow{AP} = \mu\overrightarrow{AB}\) for some scalar \(\mu\). This means that \[3\lambda \mathbf{b} - \dfrac{1}{2}\mathbf{a}(1+\lambda) = \mu(\mathbf{b}-\mathbf{a}).\]
Now any vector in the plane can be written uniquely as \(\alpha\, \mathbf{a} + \beta\, \mathbf{b}\), so we can compare the coefficients of \(\mathbf{a}\) and \(\mathbf{b}\) here, giving \[3\lambda = \mu \quad\text{and}\quad \dfrac{1}{2} + \dfrac{\lambda}{2} = \mu,\] which solve to give \[\lambda = \dfrac{1}{5}, \mu = \dfrac{3}{5}.\]
Thus
\(\lambda = \dfrac{1}{5}\)
\(\dfrac{AP}{PB} = \dfrac{\mu}{1-\mu} = \dfrac{3/5}{2/5} = \dfrac{3}{2}\).

