- A vector of magnitude \(OP\) in the direction from \(O\) to \(P\) is represented by \(\mathbf{OP}\). If \(\mathbf{OP}-3\mathbf{OQ}+2\mathbf{OR}=\mathbf{0}\), show that \(P\),\(Q\),\(R\) are collinear.
Three points with position vectors \(\mathbf{a}\), \(\mathbf{b}\) and \(\mathbf{c}\) are collinear if and only if the vectors \((\mathbf{a}-\mathbf{b})\) and \((\mathbf{a}-\mathbf{c})\) are parallel.
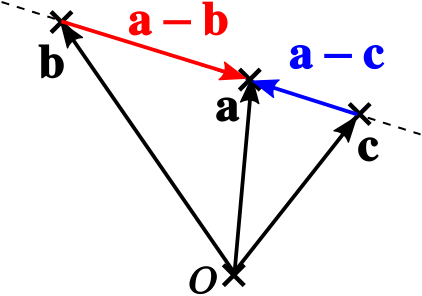
In other words, to prove collinearity, we would need to show \((\mathbf{a}-\mathbf{b})=k(\mathbf{a}-\mathbf{c})\) for some constant \(k\).
For our example, we have \(\mathbf{OP}-\mathbf{OQ}= 2(\mathbf{OQ}-\mathbf{OR})\), and so \(\mathbf{OQ}-\mathbf{OP}= -2(\mathbf{OQ}-\mathbf{OR})\), telling us that \(P, Q\) and \(R\) are collinear.
- A unit vector parallel to the \(x\)-axis is represented by \(\mathbf{i}\) and a unit vector parallel to the \(y\)-axis by \(\mathbf{j}\). If \(\mathbf{OP}=a\mathbf{i}+s\mathbf{j}\) and \(\mathbf{OQ}=-a\mathbf{i}+t\mathbf{j}\), where \(a\) is a constant and \(s\) and \(t\) are variables, show that the loci of \(P\) and \(Q\) are parallel straight lines. In this case find \(\mathbf{OQ}\) when \(\mathbf{OP}=2\mathbf{i}+3\mathbf{j}\) and \(OQ\) is perpendicular to \(OP\).
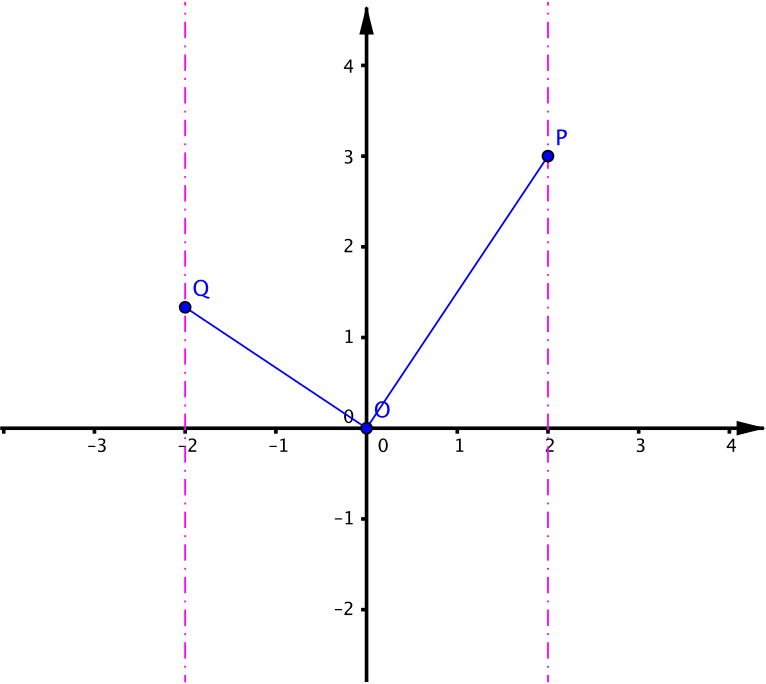
The locus of \(P\) will be the line \(x = a\), while the locus of \(Q\) will be \(x = -a\). These are parallel straight lines.
The diagram shows the case \(a = 2\). The point \(P\) is at \((2,3)\), and \(Q\) is at \((-2,k)\).
We are told that \(OP\) and \(OQ\) are perpendicular, so the gradients of \(OP\) and \(OQ\) must multiply to \(-1\).
We could alternatively use that \(\mathbf{OP}.\mathbf{OQ}=0\).
Thus \(\dfrac{3}{2} \times \dfrac{k}{-2}=-1 \implies k = \dfrac{4}{3}\). Thus \(\mathbf{OQ} = -2\mathbf{i}+\dfrac{4}{3}\mathbf{j}\).

