Given the vectors \(\mathbf{U}=\begin{pmatrix}7 \\ 6\end{pmatrix}\) and \(\mathbf{V}=\begin{pmatrix}2 \\ x\end{pmatrix}\), find the value or values of \(x\) for which
- \(\mathbf{U}\) is parallel to \(\mathbf{V}\),
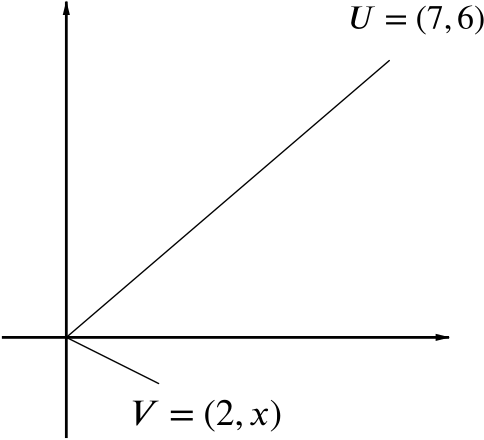
Two vectors \(\mathbf{U}\) and \(\mathbf{V}\) are parallel if and only if \(\mathbf{U}=k\mathbf{V}\) for some scalar \(k\).
This happens in our case if and only if \(7 = k \times 2\), and \(6 = k \times x\). This means \(k = 3.5\), and so \(x = \dfrac{12}{7} = 1.71 \quad (3\)sf).
Given the vectors \(\mathbf{U}=\begin{pmatrix}7 \\ 6\end{pmatrix}\) and \(\mathbf{V}=\begin{pmatrix}2 \\ x\end{pmatrix}\), find the value or values of \(x\) for which
- \(\mathbf{U}\) is perpendicular to \(\mathbf{V}\),
Two vectors in two dimensions are perpendicular if and only if their gradients multiply to \(-1\).
This happens here if and only if
\[\dfrac{6}{7} \times \dfrac{x}{2} = -1 \implies x = -\dfrac{7}{3}= -2.33 \quad (3\text{sf}).\]
Given the vectors \(\mathbf{U}=\begin{pmatrix}7 \\ 6\end{pmatrix}\) and \(\mathbf{V}=\begin{pmatrix}2 \\ x\end{pmatrix}\), find the value or values of \(x\) for which
- \(\mathbf{U}\) and \(\mathbf{V}\) have the same magnitude.
We know that the magnitude of \(\begin{pmatrix}a \\ b\end{pmatrix}\) is \(\sqrt{a^2+b^2}\).
So we need in our case to have \(\sqrt{7^2+6^2}=\sqrt{x^2+2^2}\), which gives us that \[\begin{align*} x^2 &= 7^2+6^2-2^2 \\ x &= \pm 9. \end{align*}\]We can check our answers for all three parts using the GeoGebra applet below.

