In this question we fix a real number \(\alpha\) which will be the same throughout. We say that a function \(f\) is bilateral if \[f(x) = f(2\alpha - x)\] for all \(x\).
We have \[f(x) = f(2\alpha - x) \iff f((x-\alpha)+\alpha)= f(-(x-\alpha)+\alpha),\] and so \(f(x)\) is bilateral if and only if \(x=\alpha\) is a line of symmetry for the curve \(y=f(x)\).
In the special case of \(\alpha=0\), this would mean that \(f\) is an even function.
- Show that if \(f(x) = (x-\alpha)^2\) for all \(x\) then the function \(f\) is bilateral.
If \(f(x) = (x-\alpha)^2\), then \[f(2\alpha - x) = ((2\alpha - x) -\alpha)^2 = (\alpha-x)^2 = (x-\alpha)^2 = f(x),\] for all \(x\), and so \(f\) is bilateral.
- On the other hand, if \(f(x) = x-\alpha\) for all \(x\) then the function \(f\) is not bilateral.
If \(f(x) = x-\alpha\), then \[f(2\alpha - x) = ((2\alpha - x) -\alpha) = (\alpha-x) = -f(x),\] for all \(x\), and so \(f\) is not bilateral.
The only solution to \(f(x) = -f(x)\) for all \(x\) is \(f(x) = 0\) for all \(x\), which is not the \(f(x)\) we have here.
- Show that if \(n\) is a non-negative integer and \(a\) and \(b\) are any real numbers then \[\int_a^b x^n \:dx = -\int_b^a x^n \:dx.\]
We know \(\displaystyle\int_a^b x^n \:dx = \left[\dfrac{x^{n+1}}{n+1}\right]_a^b = \dfrac{b^{n+1}-a^{n+1}}{n+1}\).
We also know that \(\displaystyle\int_b^a x^n \:dx = \left[\dfrac{x^{n+1}}{n+1}\right]_b^a = \dfrac{a^{n+1}-b^{n+1}}{n+1}\).
Thus we have that \(\displaystyle\int_a^b x^n \:dx = -\displaystyle\int_b^a x^n \:dx\).
- Hence show that if \(f\) is a polynomial (and \(a\) and \(b\) are any reals) then \[\int_a^b f(x) \:dx = -\int_b^a f(x) \:dx.\]
Let \(f(x)\) be the polynomial \(\sum\limits_{0}^{n} a_nx^n\). Then
\[\begin{align*} \int_a^b f(x) \:dx &= \int_a^b \sum_0^n a_nx^n \:dx \\ &= \sum_0^n \left(a_n\left(\int_a^b x^n \:dx\right)\right)\\ &= \sum_0^n \left(a_n\left(-\int_b^a x^n \:dx\right)\right)\\ &= -\int_b^a \sum_0^n a_nx^n \:dx\\ &= -\int_b^a f(x) \:dx. \end{align*}\]- Suppose that \(f\) is any bilateral function. By considering the area under the curve \(y = f(x)\) explain why for any \(t \geq \alpha\) we have \[\int_\alpha^t f(x) dx = \int_{2\alpha-t}^\alpha f(x) dx.\]
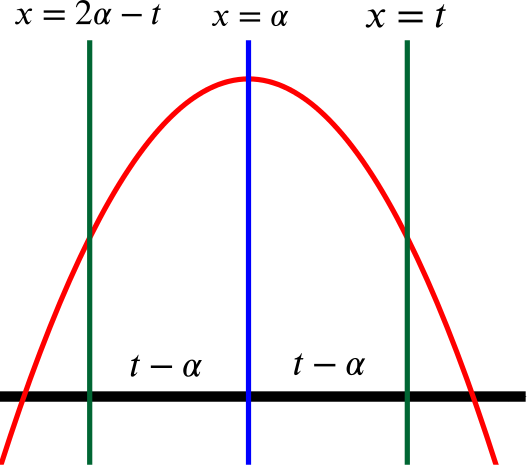
The symmetry of the bilateral function \(f(x)\) about \(x = \alpha\) guarantees that the two areas in the diagram above are equal, and so \[\int_\alpha^t f(x) \:dx = \int_{2\alpha-t}^\alpha f(x) \:dx.\]
If \(f\) is a function we write \(G\) for the function defined by \[G(t) = \int_\alpha^t f(x) \:dx\] for all \(t\).
- Suppose now that \(f\) is any bilateral function. Show that \[G(t) = -G(2\alpha-t)\] for all \(t\).
- Suppose that \(f\) is a bilateral polynomial such that \(G\) is also bilateral. Show that \(G(x) = 0\) for all \(x\).
If \(f\) is bilateral, then \(G(t) = -G(2\alpha-t)\), but if \(G\) is bilateral, then \(G(2\alpha-t)=G(t)\).
Thus on adding these equations \(G(t) = 0\) for all \(t\) (or equivalently \(G(x) = 0\) for all \(x\)).

