Prove, by considering the turning points on the graph \(y=x^3-3a^2x+b\) or otherwise, that if the equation \(x^3-3a^2x+b=0\) has three distinct real roots, then \(4a^6>b^2\).
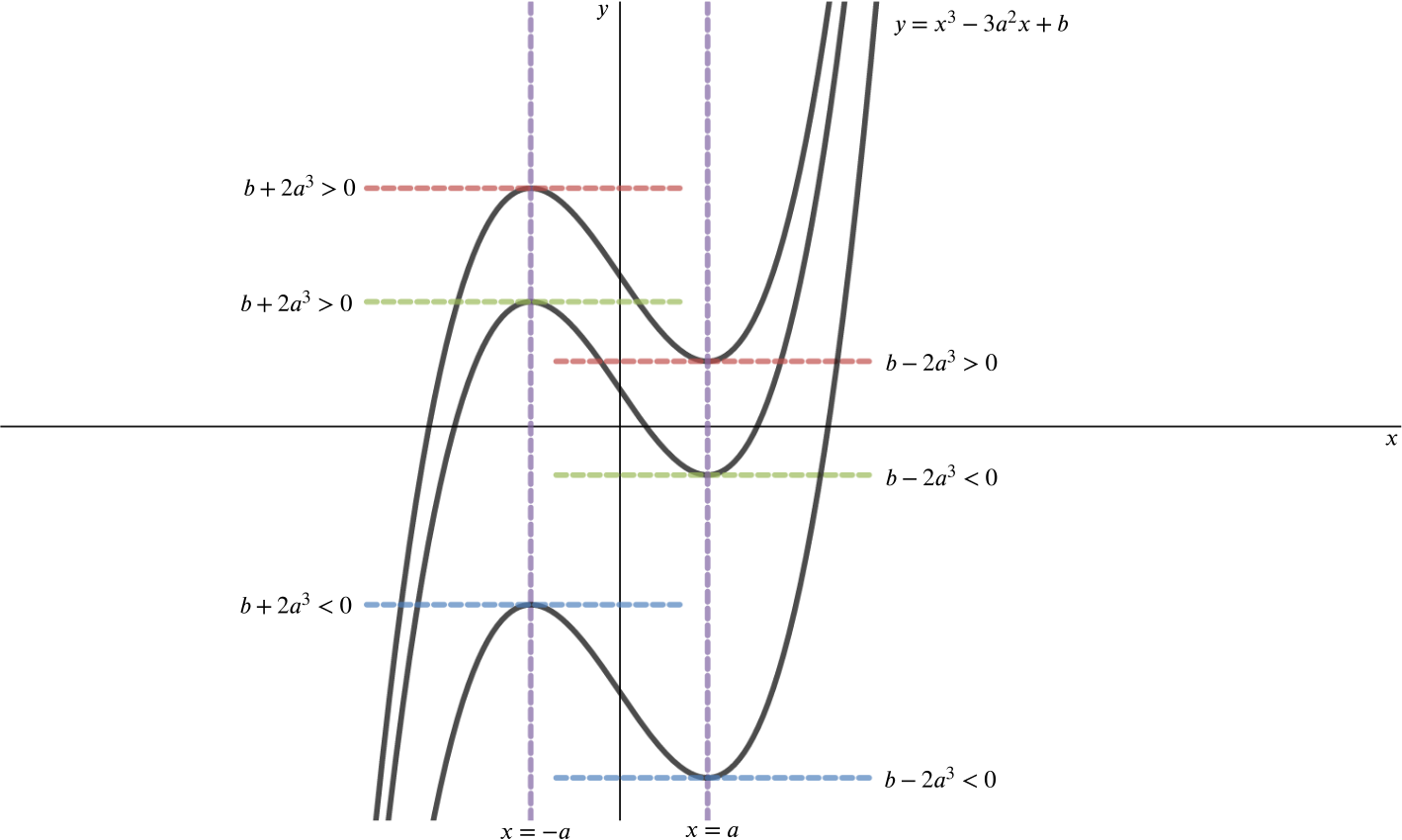
The stationary points of \(y=x^3-3a^2x+b\) occur when \[\frac{\mathrm{d}y}{\mathrm{d}x}=3x^2-3a^2=0.\] We therefore have two stationary points, at \(x=\pm a\), where \(a\neq 0\).
If \(a=0\), there is a single stationary point at \(x=0\), and it’s impossible to get three distinct roots in this case. You could try to sketch some graphs of cubic functions to see this.
Therefore, taking \(a\neq 0\), we find that the two stationary points are at \[\begin{align*} x=a, y &= a^3-3a^3 + b = -2a^3+b \\ x=-a, y &= -a^3+3a^3 + b = 2a^3+b. \end{align*}\]If the curve is to have three distinct roots, then the \(y\)-values of the stationary points must have opposite signs.
So EITHER \[-2a^3+b >0\,\, \text{and} \,\, 2a^3+b < 0, \,\, \text{which gives} \,\, 2a^3 < b < -2a^3,\] OR \[-2a^3+b < 0\,\, \text{and} \,\, 2a^3+b > 0, \,\, \text{which gives}\,\, -2a^3 < b < 2a^3.\]
The first of these is only possible if \(a\) is negative, while the second is only possible if \(a\) is positive. In either case, we can combine these inequalities to get \(b^2 < 4a^6\).
The graph below shows the situation if \(a\) is positive.