When is $f(x) = 2x^3 − 9x^2 + 12x + 3$ smallest over this range?

Add to your resource collection Remove from your resource collection Add notes to this resource View your notes for this resource

The smallest value will occur either at a stationary point of \(f(x)\), or at one of the endpoints of the range, \(x = 0\) or \(x = 2\).

To find stationary points, we solve \(f'(x) = 6x^2 - 18x + 12 = 0\), or equivalently \(0 =x^2 - 3x + 2 = (x - 1)(x - 2)\).

So \(x = 1\) and \(x = 2\) are the stationary points of \(f(x)\), and are in the desired range. From our knowledge of the shape of cubics, or from looking at \(f''(x)\), we know that \(x = 1\) is a maximum and \(x = 2\) is a minimum.

Then the minimum value of \(f(x)\) is either at \(x = 2\) or \(x = 0\), so we can check the values. We have \[\begin{align*} f(2) &= 16 - 36 + 24 + 3 = 7 \\ f(0) &= 3. \end{align*}\]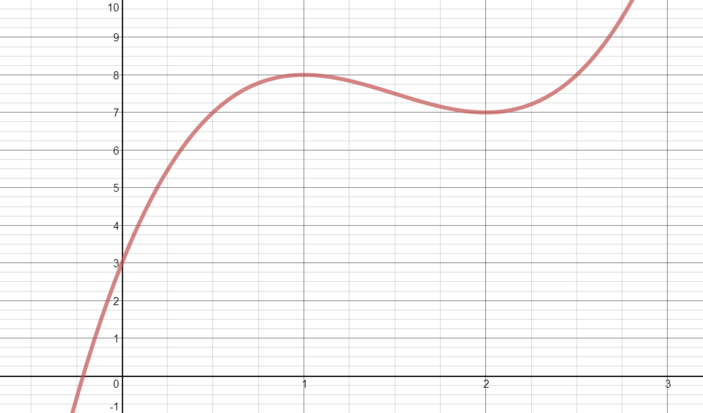

So the minimum value of \(f(x)\) for \(0 \leq x \leq 2\) is \(3\), and the answer is (b).