Let \[\quad f(x) = \begin{cases}x+1 & \text{for } 0 \leq x \le 1; \\ 2x^2-6x+6 & \text{for } 1 \leq x \le 2. \end{cases}\]
- Sketch a graph of \(y=f(x)\) for \(0 \le x \le 2\), labelling any turning points and the values attained at \(x=0\), \(1\), \(2\).
There is no turning point in the interval \(0 \le x \le 1\). To find any turning points in the interval \(1 \le x \le 2\), we first differentiate \(f(x)\) in this interval to get \[f'(x) = 4x - 6.\] Setting \(f'(x)=0\) gives \(x=\dfrac{3}{2}\), so there is just one turning point, at \(\left(\dfrac{3}{2},\dfrac{3}{2}\right)\).
We also have \[ f(0) = 1; \quad f(1) = 2; \quad f(2) = 2. \]
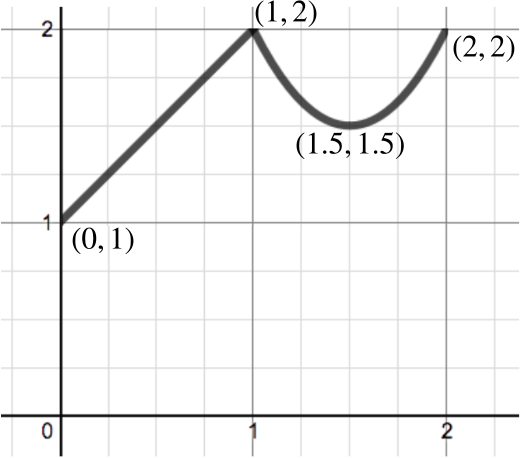
We could alternatively find the turning point for the quadratic section by completing the square. We have \(2x^2-6x+6= 2(x - 3/2)^2 + 3/2\).
- For \(1 \le t \le 2\), define \[g(t) = \int_{t-1}^{t} f(x) \:dx.\] Express \(g(t)\) as a cubic in \(t\).
Note \(\displaystyle\int_{t-1}^{1} x+1 \:dx = \left[\dfrac{x^2}{2}+x\right]_{t-1}^{1}= \left[\dfrac{(x+1)^2}{2}\right]_{t-1}^{1}\).
- Calculate and factorise \(g'(t)\).
- What are the minimum and maximum values of \(g(t)\) for \(t\) in the range \(1 \le t \le 2\)?
The minimum and maximum values will occur either at the end points (\(t=1\) or \(t=2\)) or at the turning points.
The turning points occur when \(g'(t)=0\), which is when \(t=\dfrac{3}{2}\) or \(t=2\).
We have \[\begin{align*} g(1) &= \dfrac{3}{2} = \dfrac{36}{24}; \\ g\left(\dfrac{3}{2}\right) &= \dfrac{41}{24}; \\ g(2) &= \dfrac{5}{3} = \dfrac{40}{24}. \end{align*}\]So the maximum occurs at \(t=\dfrac{3}{2}\) with value \(\dfrac{41}{24}\), and the minimum is at \(t=1\) with value \(\dfrac{3}{2}\).

