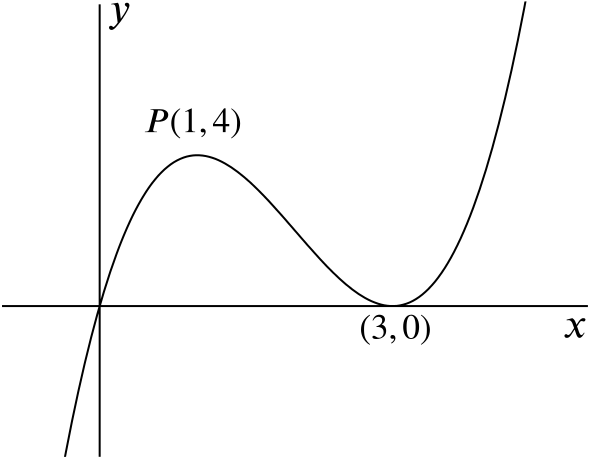
Show that the gradient of the curve \(y=x(x-3)^2\) is zero at the point \(P(1,4)\), and sketch the curve.
Thus \(\dfrac{dy}{dx}=0\) when \(x=1\) and when \(x=3\). At \(x=1\), \(y=4\); at \(x=3\), \(y=0\).
So the gradient of the curve is zero at \(P(1,4)\) and also at \((3,0)\).
To sketch the curve, we note that the roots occur at \(x=0\) and \(x=3\) (with the latter being a double root, and so the curve touches the \(x\)-axis here). The \(y\)-intercept is \(0\).
The equation is a cubic with \(x^3\) as the leading term. So as \(x \to\infty\), \(y\to\infty\), and as \(x\to-\infty\), \(y\to-\infty\).
So the stationary point at \(P(1,4)\) must be a maximum, and that at\((3,0)\) must be a minimum, giving
The tangent at \(P\) cuts the curve again at \(Q\). Calculate the areabetween the chord \(PQ\) and the curve.
The tangent at \(P\) has equation \(y=4\). This intersects the cubic again when \[4 = x(x-3)^2.\] We can expand this and rearrange to get \[x^3-6x^2+9x-4=0.\] We already know that \(x=1\) is a double root of this equation (as the line \(y=4\) touches the curve at \(x=1\)), so \((x-1)^2\) will be a factor. We can factorise to give \[(x-1)(x^2-5x+4)=0\] so \[(x-1)^2(x-4)=0.\]
We could have written this down immediately, since the factorisation must be \((x-1)^2(x-a)\) for some \(a\), which will expand to \(x^3+px^2+qx-a\) for some \(p\) and \(q\), and so \(a\) must be \(4\) to match the constant terms.
Thus the tangent at \(P\) intersects the curve again at \(Q(4,4)\). We can now calculate the required area, indicated by \(R\) on this sketch.
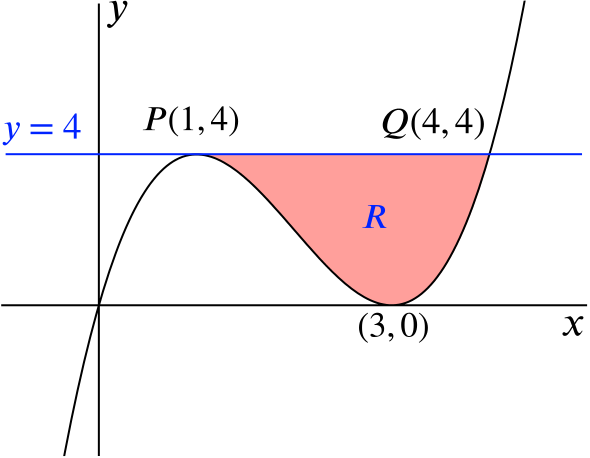
Thus the area of \(R\) is \(12-\dfrac{21}{4}=\dfrac{27}{4}=6\dfrac{3}{4}\).

