Let \(f(x) = x^3 + ax^2 + bx + c\), where the coefficients \(a\), \(b\) and \(c\) are real numbers. The figure below shows a section of the graph of \(y=f(x)\). The curve has two distinct turning points; these are located at \(A\) and \(B\), as shown. (Note that the axes have been omitted deliberately.)
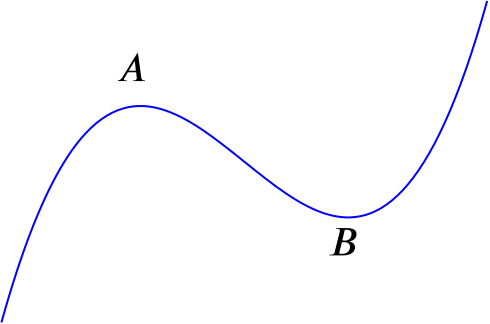
- Find a condition on the coefficients \(a\), \(b\), \(c\) such that the curve has two distinct turning points if, and only if, this condition is satisfied.
It may be assumed from now on that the condition on the coefficients in (i) is satisfied.
Let \(x_1\) and \(x_2\) denote the \(x\) coordinates of \(A\) and \(B\), respectively. Show that \[x_2 - x_1 = \frac{2}{3} \sqrt{a^2 - 3b}.\]
Suppose now that the graph of \(y=f(x)\) is translated so that the turning point at \(A\) now lies at the origin. Let \(g(x)\) be the cubic function such that \(y=g(x)\) has the translated graph. Show that \[g(x) = x^2 \left(x - \sqrt{a^2 - 3b}\right).\]
Let \(R\) be the area of the region enclosed by the \(x\)-axis and the graph \(y=g(x)\). Show that if \(a\) and \(b\) are rational then \(R\) is also rational.
Is it possible for \(R\) to be a non-zero rational number when \(a\) and \(b\) are both irrational? Justify your answer.

