Find the coordinates of the turning point on the curve \(y=x^2-2bx+c\).
We have that \[ \frac{dy}{dx}=2x-2b, \] so the turning point is at \(x=b\), which gives \(y=b^2-2b^2+c=c-b^2\). Therefore the turning point is at \((b,c-b^2)\).
Sketch the curve in the case that the equation \(x^2-2bx+c=0\) has two distinct real roots.
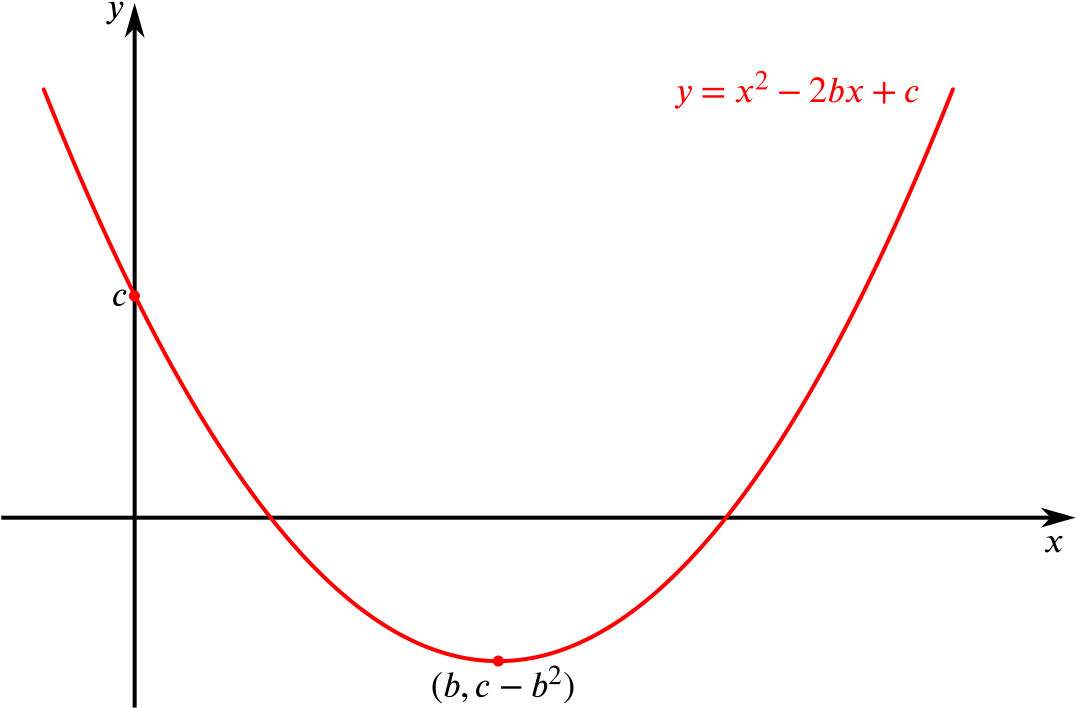
Use your sketch to determine necessary and sufficient conditions on \(b\) and \(c\) for the equation \(x^2-2bx+c=0\) to have two distinct real roots.
We can see from our sketch that as long as the turning point lies below the \(x\)-axis, the curve will meet the \(x\)-axis in two different places and hence \(y=0\) will have two distinct real roots.
That is, we must have \(c-b^2<0\) in order to have two distinct real roots of \(x^2-2bx+c=0\).
This condition is necessary and sufficient.
Determine necessary and sufficient conditions on \(b\) and \(c\) for this equation to have two distinct positive roots.
We’d like to see when these distinct real roots are also positive. Firstly, in order for us to have a chance of this happening, we must have \(b>0\).
Imagine shifting a parabola along the \(x\)-axis like in this picture:
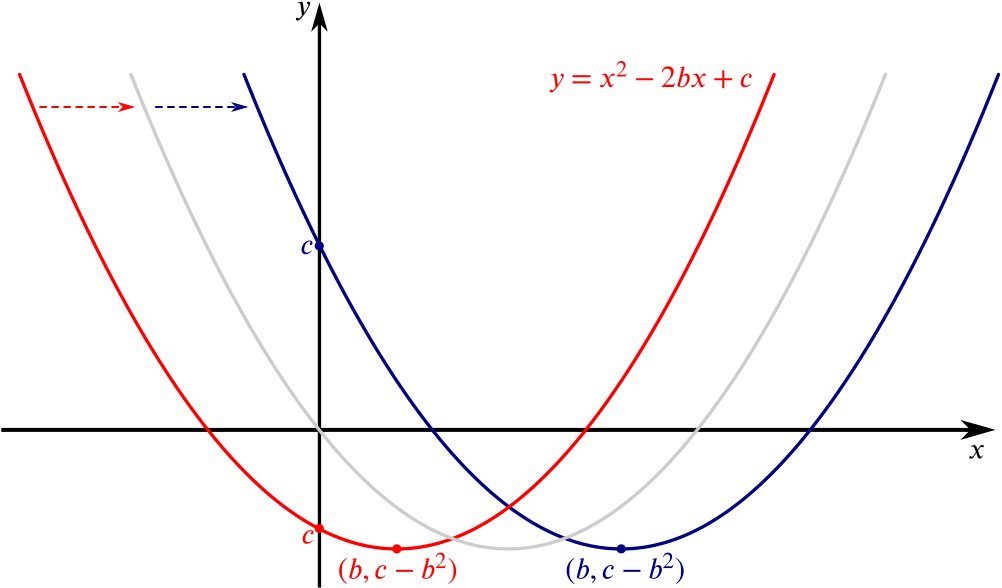
Notice that, provided \(b>0\), the sign of \(c\) determines whether or not both roots are positive.
If we already know that we have two distinct positive roots, the parabola must cut the \(y\)-axis before \(x\) reaches the value of the smallest root.
Therefore, the necessary and sufficient conditions for \(x^2-2bx+c=0\) to have two distinct positive roots are \[\begin{align*} c-b^2<0, \\ b>0, \\ c>0. \end{align*}\] In fact we can combine the first and last of these to give \[\begin{align*} b>0, \\ b^2>c>0. \end{align*}\]We’ve derived these conditions by looking at our sketches, as the question asked. We could double-check these results using the quadratic formula.
From the quadratic formula the roots of the equations are \(x = b \pm\sqrt{b^2 - c}.\) The roots are both real if and only if \(b^2>c\). In addition, both roots are positive if and only if \(b > 0\) and \(b > \sqrt{b^2-c}\) (which implies \(c>0\)). Therefore we have two positive roots if and only if \(b>0\) and \(b^2>c>0\), as before.
Find the coordinates of the turning points on the curve \(y=x^3-3b^2x+c\) (with \(b>0\)) and hence determine necessary and sufficient conditions on \(b\) and \(c\) for the equation \(x^3-3b^2x+c=0\) to have three distinct real roots.
We have that \[ \frac{dy}{dx}=3x^2-3b^2=0 \iff x=\pm b. \] So the turning points on \(y\) are \((b,b^3-3b^3+c)=(b,c-2b^3)\) and \((-b,-b^3+3b^3+c)=(-b,c+2b^3)\).
To determine the conditions on \(b\) and \(c\) for \(y=0\) to have three distinct real roots, let’s sketch \(y\) as we did for the quadratic case.
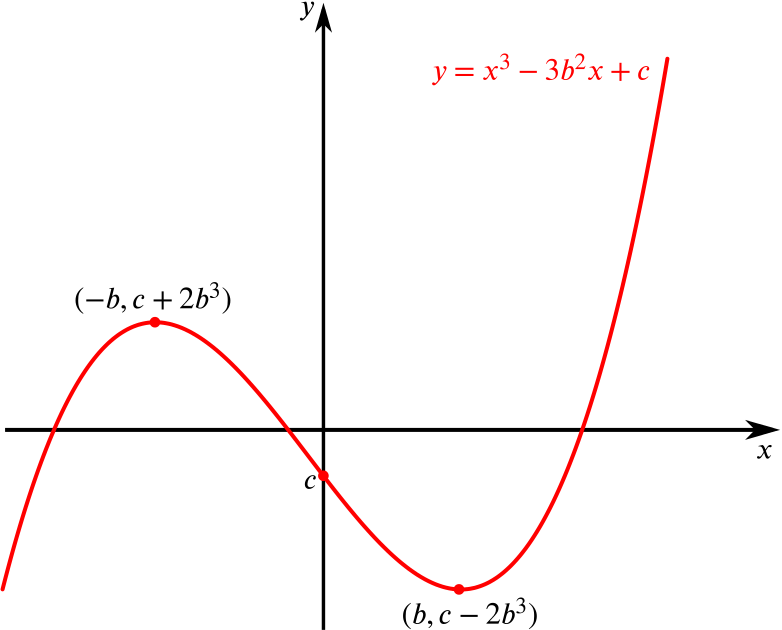
We see \(y\) will have three distinct real roots as long as the turning points lie with one above the \(x\)-axis and one below the \(x\) axis.
Since \(b>0\), this condition is \(2b^3+c>0\) and \(c-2b^3<0\), or \(-2b^3 < c < 2b^3\). We can combine these inequalities into \(c^2 < 4b^6\).
Determine necessary and sufficient conditions on \(a\), \(b\) and \(c\) for the equation \((x-a)^3-3b^2(x-a)+c=0\) to have three distinct positive roots.
Let’s sketch \(y=(x-a)^3-3b^2(x-a)+c\) on the same axis as our previous sketch. This is just a shift of \(a\) in the \(x\)-direction, so our sketch becomes
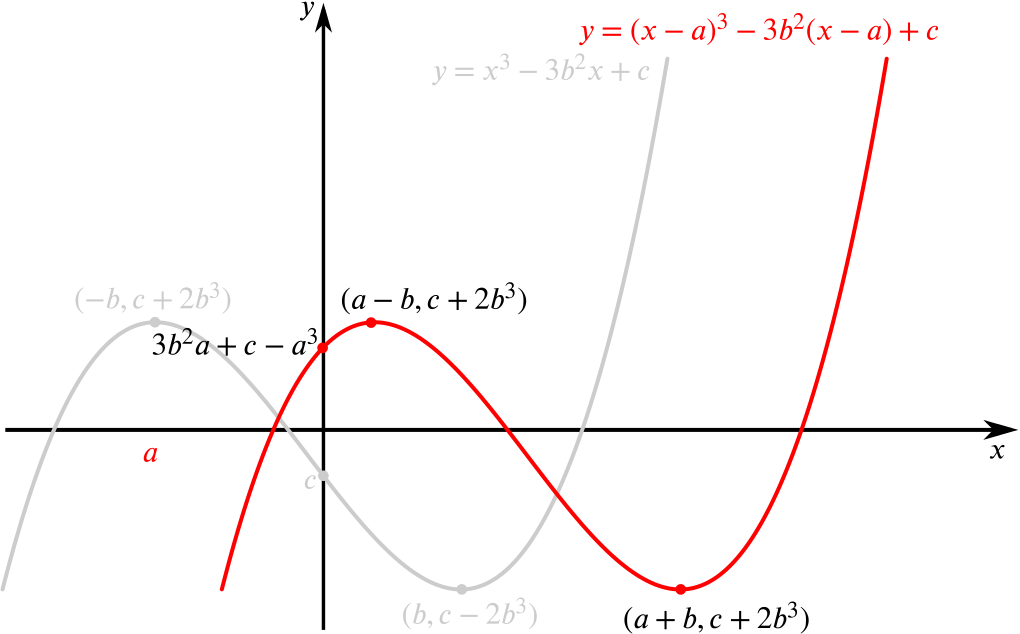
Examining our sketch, we certainly need both turning points to have positive \(x\)-coordinates if we want the roots to be positive, and so we need \(a > b\).
We see also that the graph must cross the \(y\)-axis before the smallest root, which means that we must have a negative \(y\)-intercept. The \(y\)-intercept comes from the constant terms, which can be found by looking at the last term in the expansion of each bracket (there’s no need to do the full expansion, we can just think about the constant). Therefore we need \(-a^3+3ab^2+c<0\) if the cubic is to have three positive roots. (In the diagram above the \(y\)-intercept is positive and you can see that the cubic has a negative root.)
We determined earlier the condition for the cubic to have three distinct real roots, namely \(c^2 < 4b^6\).
Show that the equation \(2x^3-9x^2+7x-1=0\) has three distinct positive roots.
Since we just established conditions for a cubic in a certain form to have three distinct positive roots, we should try to write \(2x^3-9x^2+7x-1\) in this form, so that we can check if these conditions hold.
We seek \(a,b\) and \(c\) such that \[ 2x^3-9x^2+7x-1=2[(x-a)^3-3b^2(x-a)+c]. \] Let’s multiply out the brackets on the right hand side. \[ (x-a)^3-3b^2(x-a)+c=x^3-3ax^2+3a^2x-a^3-3b^2x+3b^2a+c, \] so we have \[ 2x^3-9x^2+7x-1=2[x^3-3ax^2+(3a^2-3b^2)x-a^3+3b^2a+c]. \] From this we can see that \(9=6a\), \(7=6a^2-6b^2\) and \(-1=2c-2a^3+6b^2a\).
We can easily solve the first equation to see that \(a=\dfrac{3}{2}\).
The second equation becomes \[ 7=6\times\frac{9}{4}-6b^2, \] and so \[ 6b^2=\frac{13}{2}, \] which tells us that \[ b=\sqrt{\frac{13}{12}}. \] Finally, we must solve \[ -1=2c-2\times\left(\frac{3}{2}\right)^3+\frac{13}{2}\times\frac{3}{2}. \] Rearranging, we find that \[ 2c=-1+\frac{27}{4}-\frac{39}{4}=-1-\frac{12}{4}=-4, \] so that \(c=-2\).
Therefore we can write \[ 2x^3-9x^2+7x-1=2\left[\left(x-\frac{3}{2}\right)^3-\frac{13}{4}\left(x-\frac{3}{2}\right)-2\right]. \] Now we can check that the conditions we gave earlier are satisfied.
We have \(a = 1.5 > \sqrt{\dfrac{13}{12}} = b\) and \(c^2= 4 < 4\left(\sqrt{\dfrac{13}{12}}\right)^6 = 4b^6\).
Also \(-a^3+3ab^2+c=-\dfrac{27}{8}+3 \left( \dfrac{3 \times 13}{2 \times 12} \right) -2=-\dfrac{17}{8}<0\),
So the equation has three distinct positive real roots.

