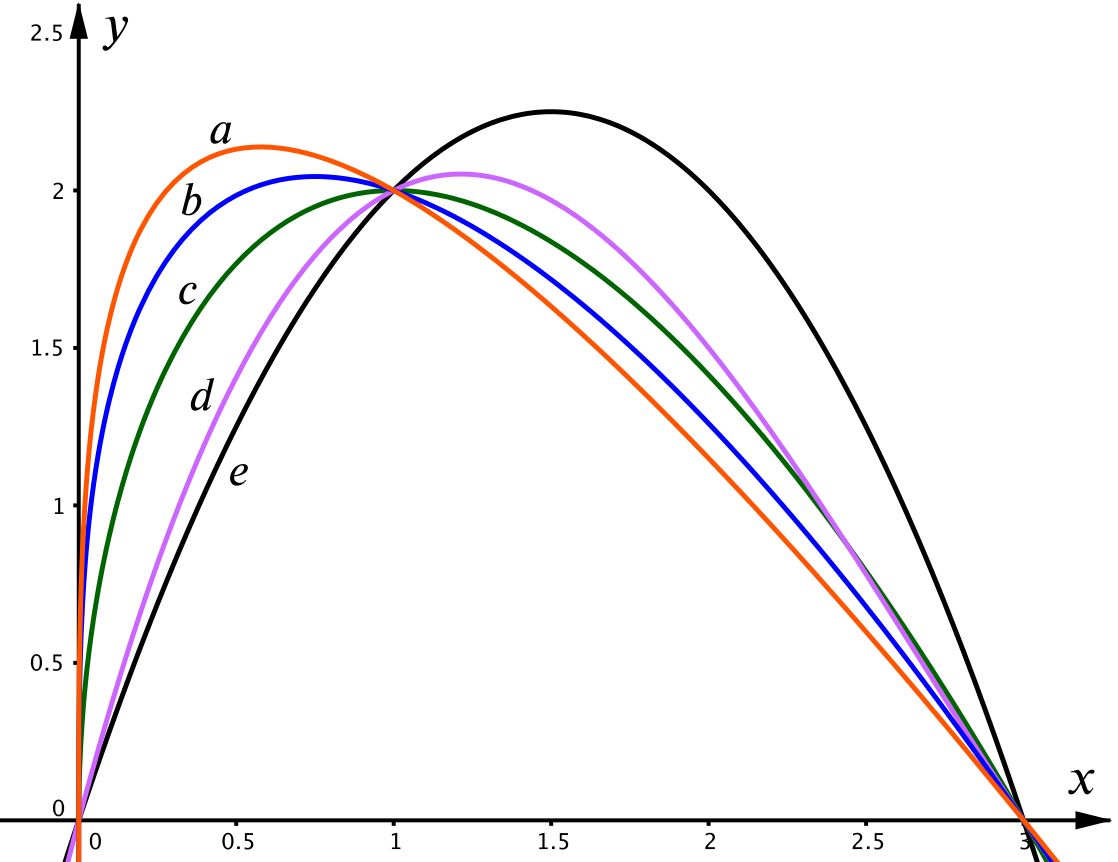
This graph shows five curves, \(a\), \(b\), \(c\), \(d\) and \(e\), which all pass through the origin and the points \((1,2)\) and \((3,0)\). They each have one local maximum between \(x=0\) and \(x=3\).
Below are the equations of the five curves plus one extra equation. Find the coordinates of the maxima and hence identify which equation goes with which curve.
| \(y=x(3-x)\) | \(y=\sqrt[3]x(3-x)\) | |
| \(y=\sqrt x(3-x)\) | \(y=\dfrac{1}{6}x(3-x)(5+x)\) | |
| \(y=\dfrac{1}{4}x(3-x)(5-x)\) | \(y=\dfrac{2}{\sqrt[3] 9 -1} \left( \sqrt[3]{9x} -x \right)\) |
Add a sketch of the missing curve on the same axes.

