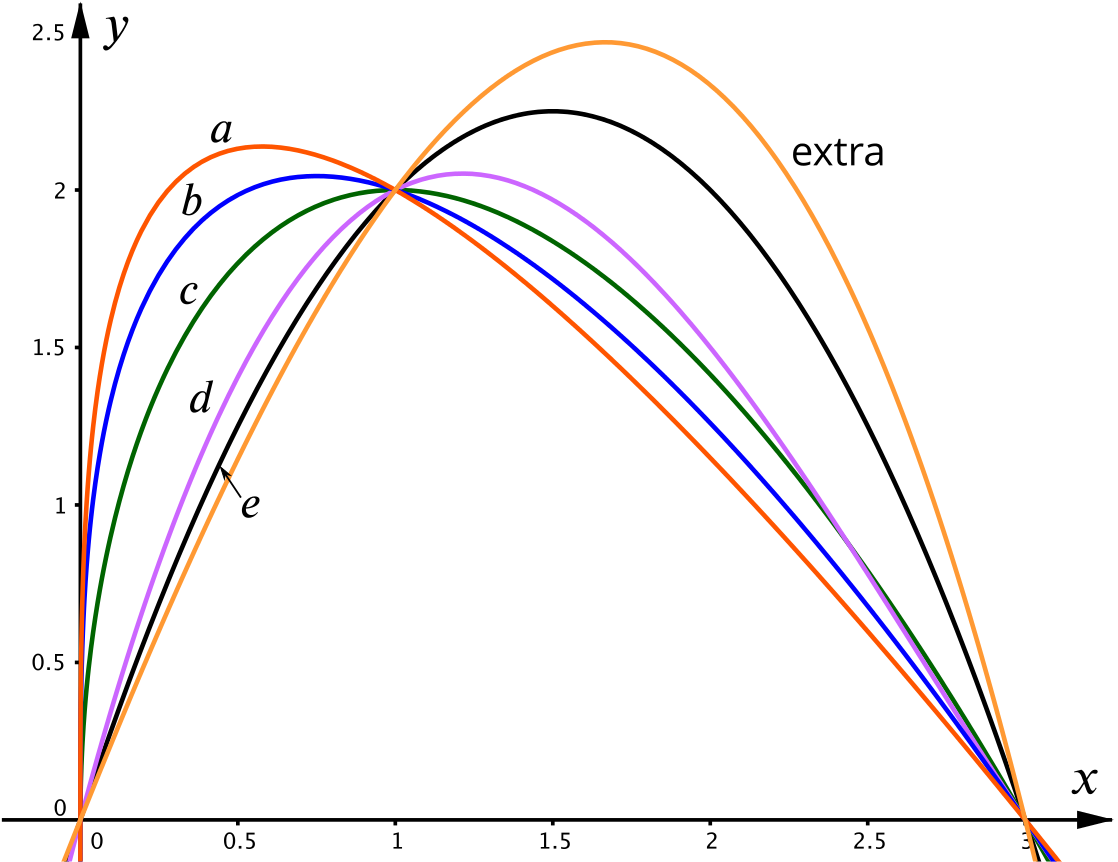
Below are the equations of the five curves plus one extra equation. Find the coordinates of the maxima and hence identify which equation goes with which curve.
To find the coordinates of the maximum of each curve, we can differentiate each equation. This gives us a formula for the gradient and this is zero at the maximum.
\(y=x(3-x)\)
Setting \(\frac{dy}{dx}=0\) gives us \(3-2x=0\) and hence \(x=\frac{3}{2}\). The black curve, \(e\), appears to have a maximum at \(x=1.5\), suggesting that this is the equation of \(e\).
This equation is a quadratic, so we could have located it’s maximum without using calculus.
\(y=\sqrt x(3-x)\)
So this is the green curve, \(c\).
\(y=\dfrac{1}{4}x(3-x)(5-x)\)
Setting the gradient equal to zero gives us a quadratic equation with roots \(x=\dfrac{8}{3}\pm\dfrac{\sqrt{19}}{3}\). The one of these roots that is between zero and three is at \(x\approx1.21\), so this appears to be the purple curve, \(d\).
\(y=\sqrt[3]x(3-x)\)
So this appears to be the blue curve, \(b\).
\(y=\dfrac{1}{6}x(3-x)(5+x)\)
As above, we have a quadratic equation which factorises to give \(x=-3\) or \(\frac{5}{3}\). The black curve, \(e\), has a maximum close to \(x=\frac{5}{3}\), but we have already suggested the first equation for this curve. The first equation does look a better fit, but to check we could calculate the \(y\) values of the two candidates at their maxima and see which ones matches.
The first equation at \(x=\frac{3}{2}\) gives \(y=\frac{9}{4}=2.25\).
This equation at \(x=\frac{5}{3}\) gives \(y=\frac{200}{81}\approx2.5\).
The first equation is definitely a better match for curve \(e\), so this equation is the one without a graph.
\(y=\dfrac{2}{\sqrt[3] 9 -1} \left( \sqrt[3]{9x} -x \right)\)
By elimination, this must be the remaining curve, \(a\), but let’s do the calculation to be sure.
\[\begin{align*} y &= \frac{2}{\sqrt[3] 9 -1} \left( \sqrt[3]{9}x^\frac{1}{3} -x \right)\\ \frac{dy}{dx} &= \frac{2}{\sqrt[3] 9 -1} \left( \frac{\sqrt[3]{9}}{3}x^{-\frac{2}{3}} -1 \right) \end{align*}\] So at the maximum, \[\begin{align*} \frac{\sqrt[3]{9}}{3}x^{-\frac{2}{3}} -1 &= 0\\ x^{\frac{2}{3}} &= \frac{\sqrt[3]{9}}{3}\\ x^2 &= \frac{9}{3^3} = \frac{1}{3}\\ x &= \pm \frac{1}{\sqrt{3}} \approx \pm 0.58 \end{align*}\]This does indeed match graph \(a\).
Add a sketch of the missing curve on the same axes.