Meaningful areas

Add to your resource collection Remove from your resource collection Add notes to this resource View your notes for this resource

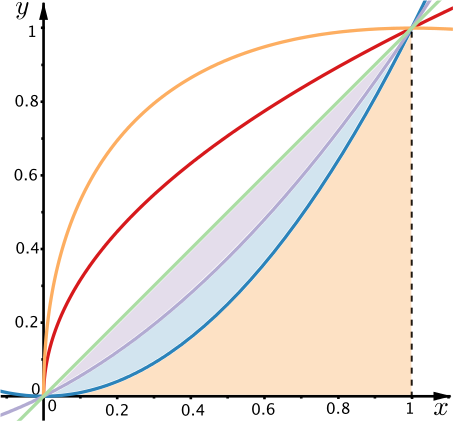
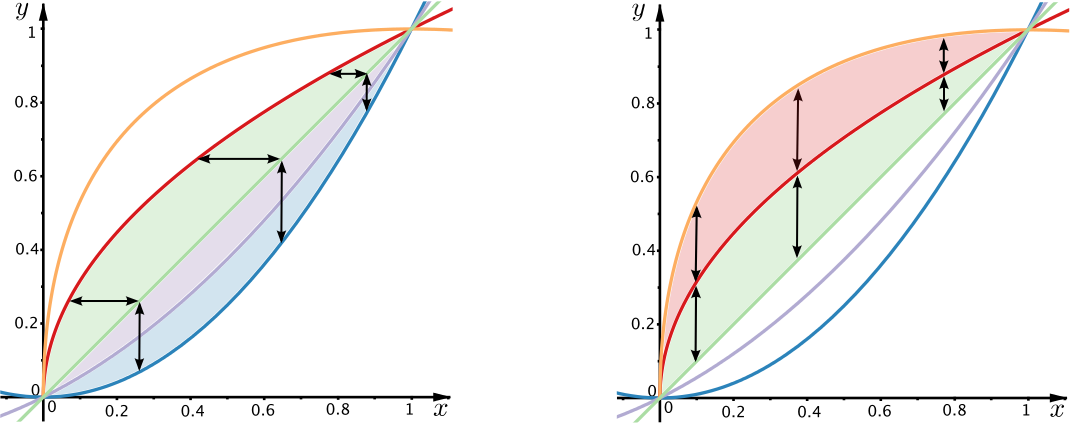In Curve match we asked you to match the curves on the diagram below with the following functions.

\[ y=\sqrt{x} \quad y=x^2 \quad y=x \quad y=\dfrac{x^2+x}{2} \quad \text{and } \quad y=2\sqrt{x}-x\]

Now we’d like you to look at the different regions enclosed by the curves.

• Which do you think is the smallest region? How can you check?

Think about what techniques you can use and how you can reduce the number of calculations you need to do.

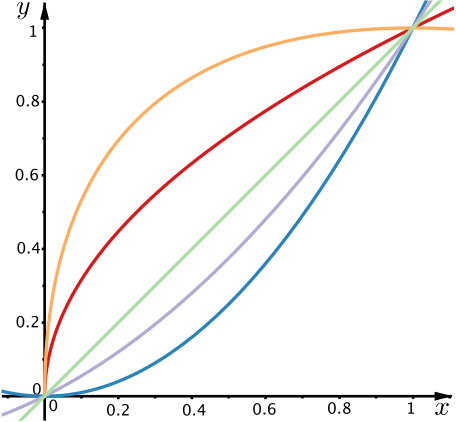
It looks as if the region between \(y=\dfrac{x^2+x}{2}\) and \(y=x^2\) or the region between \(y=x\) and \(y=\dfrac{x^2+x}{2}\) could be the smallest, but it’s difficult to tell which is smaller just by looking.

One way to check which region is smaller is to use integration to find the areas. In order to find the area enclosed by \(y=\dfrac{x^2+x}{2}\) and \(y=x^2\) we could first find the area under \(y=\dfrac{x^2+x}{2}\), the upper boundary of the region, and subtract the area under the \(y=x^2\), the lower boundary of the region we want. However, because integration is linear, we could instead integrate the difference beween the two functions, as follows.

\[\int_{0}^{1} \dfrac{x^2+x}{2} -x^2\, dx = \int_{0}^{1} \dfrac{x-x^2}{2}\, dx = \int_{0}^{1} \dfrac{x}{2}-\dfrac{x^2}{2}\, dx = \left[ \dfrac{x^2}{4}-\dfrac{x^3}{6}\right]_{0}^{1} = \left(\dfrac{1}{4}-\dfrac{1}{6}\right) = \dfrac{1}{12}\]

Similarly, the area of the region between \(y=x\) and \(y=\dfrac{x^2+x}{2}\) is given by

\[\int_{0}^{1} x-\dfrac{x^2+x}{2}\, dx = \int_{0}^{1} \dfrac{x-x^2}{2}\, dx\]

What does this tell you? Can you explain it?

You may have found that the areas of regions in the diagram can be found in several ways. We will illustrate a few of these here.

Using symmetry

Now that we know the size of the blue and purple regions, we can do some calculations based on symmetry.

For example, we know that \(y=\sqrt{x}\) and \(y=x^2\) (for the section of the graph shown) are reflections of each other in the line \(y=x\) because they are the graphs of inverse functions. Therefore the area between \(y=\sqrt{x}\) and \(y=x\) is the same as the area between \(y=x\) and \(y=x^2\), which is the sum of the areas of the blue and purple regions.

Using composite shapes

From the diagram we can see that the area of the region between \(y=x\), the \(x\)-axis and the line \(x=1\) is \(\tfrac{1}{2}.\) Therefore the area between \(y=x^2\) and the \(x\)-axis is \(\tfrac{1}{3}.\)

Using means

We used symmetry about the line \(y=x\) to calculate the area of the region between \(y=\sqrt{x}\) and \(y=x.\) Even though \(y=2\sqrt{x}-x\) and \(y=\sqrt{x}\) are not the graphs of inverse functions, we can use a symmetry-based argument to explain why the region between \(y=2\sqrt{x}-x\) and \(y=\sqrt{x}\) is the same size as the region between \(y=\sqrt{x}\) and \(y=x.\) In this case, we are using symmetry about a mean value, and the following diagram illustrates these two uses of symmetry.

Can you use this idea to explain why the region between \(y=x\) and \(y=\dfrac{x^2+x}{2}\) is the same size as the region between \(y=\dfrac{x^2+x}{2}\) and \(y=x^2\)?

Further things to investigate

• The area of the region between \(y=x^2\), the \(x\)-axis and the line \(x=1\) is \(\tfrac{1}{3}.\) Can we find a function whose graph splits this region into areas of \(\tfrac{1}{6}\)?

• Can you find other functions whose graphs pass through \((0,0)\) and \((1,1)\) and bound regions of area \(\tfrac{1}{12}\)?