The curve \(C\) has equation \(xy=\dfrac{1}{2}\). The tangents to the curve \(C\) at the distinct points \(P(p,\dfrac{1}{2p})\) and \(Q(q,\dfrac{1}{2q})\), where \(p\) and \(q\) are positive, intersect at \(T\) and the normals to \(C\) at these points intersect at \(N\). Show that \(T\) is the point \[\left(\dfrac{2pq}{p+q},\dfrac{1}{p+q}\right).\]
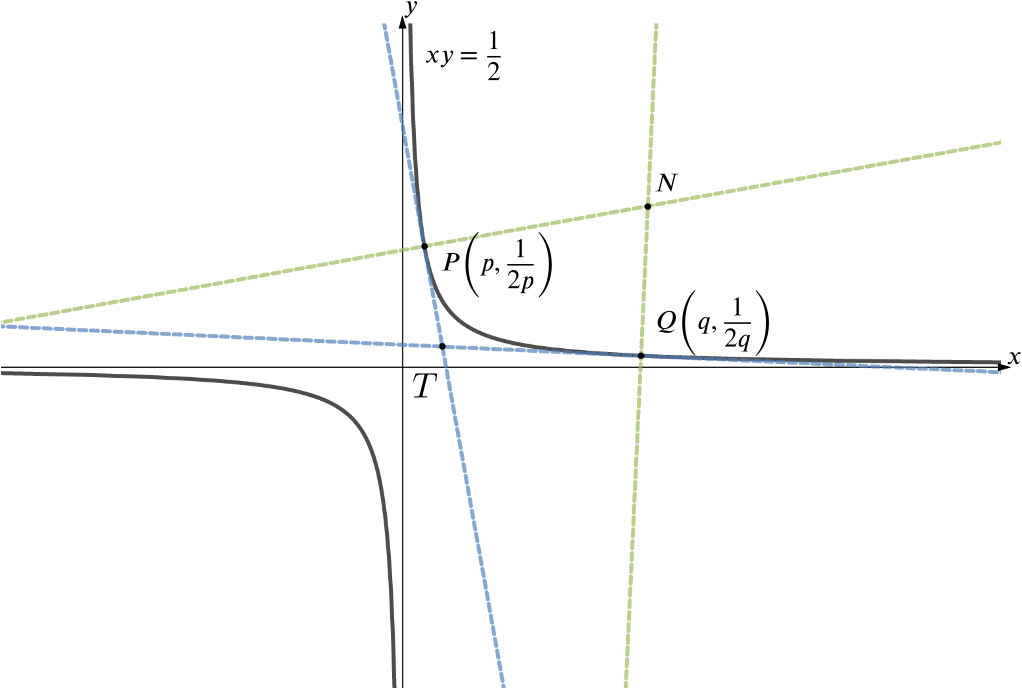
We have the points \(P(p,\dfrac{1}{2p})\) and \(Q(q,\dfrac{1}{2q})\) where, without loss of generality, \(0< p< q\) as in the diagram. We can rearrange the equation of the curve to \(y = \dfrac{1}{2x}\) and then differentiate to obtain
\[\frac{dy}{dx} = -\frac{1}{2x^2}.\]
At the point \(P\), with coordinates \((p, \dfrac{1}{2p})\), the gradient is therefore \(-\dfrac{1}{2p^2}\). Thus the equation of the tangent through \(P\) is \[\left(y-\frac{1}{2p}\right)=-\frac{1}{2p^2}(x-p),\] that is, \[y=\frac{1}{p}-\frac{1}{2p^2}x.\] Similarly, the equation of the tangent through \(Q\) is \(y=\dfrac{1}{q}-\dfrac{1}{2q^2}x.\)
The two tangents intersect when \[\frac{1}{p}-\frac{1}{2p^2}x=\frac{1}{q}-\frac{1}{2q^2}x.\] i.e. when \[x\left(\frac{1}{2q^2}-\frac{1}{2p^2}\right) = \frac{1}{q}-\frac{1}{p},\] We can simplify the left-hand bracket, using the difference of two squares, to give \[\frac{1}{2q^2}-\frac{1}{2p^2}=\frac{1}{2} \left(\left(\frac{1}{q}\right)^2 -\left(\frac{1}{p}\right)^2\right) = \frac{1}{2}\left(\frac{1}{q}-\frac{1}{p}\right)\left(\frac{1}{q} + \frac{1}{p}\right) = \frac{1}{2}\left(\frac{1}{q}-\frac{1}{p}\right)\left(\frac{p+q}{pq} \right).\] Then the equation involving the \(x\)-coordinate of \(T\) simplifies to \[\frac{1}{2} x \left(\frac{1}{q}-\frac{1}{p}\right)\left(\frac{p+q}{pq} \right) = \left(\frac{1}{q}-\frac{1}{p}\right)\] and so, dividing through by the bracketed expression on both sides (which is not zero since \(p \neq q\)) and making \(x\) the subject, we see that \[x = \frac{2pq}{p+q}.\] The \(y\)-coordinate of \(T\) is then \[\begin{align*} y&=\dfrac{1}{p}-\dfrac{1}{2p^2}\times\dfrac{2pq}{p+q}\\ &=\dfrac{1}{p}\left(1-\dfrac{q}{p+q}\right)=\dfrac{1}{p+q}, \end{align*}\]as required.
In the case \(pq=\dfrac{1}{2}\), find the coordinates of \(N\).
It would be helpful to find the equations of the normals to the curve at \(P\) and \(Q\).
We know that (gradient of the normal) \(\times\) (gradient of the tangent) at any point on the curve is \(-1\).
We can therefore use what we know about the gradients of the tangents to the curve at \(P\) and \(Q\).
The gradients of the normals through \(P\) and \(Q\) are \(2p^2\) and \(2q^2\), respectively. The equation of the normal through \(P\) is therefore \[\left(y-\frac{1}{2p}\right)=2p^2(x-p),\] which we can rearrange to give \[y=2p^2x+\frac{1}{2p}-2p^3.\] Similarly, the normal through \(Q\) has equation \[y = 2q^2x + \frac{1}{2q} - 2q^3.\]
The two normals intersect at \(N\), whose \(x\) coordinate satisfies \[2p^2x+\frac{1}{2p}-2p^3=2q^2x+\frac{1}{2q}-2q^3,\] that is, \[\begin{align*} 2(p-q)(p+q)x &= \dfrac{1}{2}\left(\dfrac{1}{q}-\dfrac{1}{p}\right)+2(p^3-q^3)\\ &= \dfrac{1}{2}\left(\dfrac{p-q}{pq}\right)+2(p-q)(p^2+pq+q^2) \end{align*}\]and so \[x = \frac{1}{p+q}\left(\frac{1}{4pq}+p^2+pq+q^2\right). \qquad (p\neq q)\]
Using \(pq=\dfrac{1}{2}\), this becomes \[\begin{align*} x&=\dfrac{1}{p+q}\left(\dfrac{(pq)^2}{pq}+p^2+pq+q^2\right)\\ &=\dfrac{1}{p+q}\left(p^2+2pq+q^2\right)\\ &=\dfrac{1}{p+q}(p+q)^2\\ &=p+q. \end{align*}\]Substituting back into the equation of the normal through \(P\) we find \[y=2p^2(p+q)+\frac{1}{2p}-2p^3=2p^2q+\frac{1}{2p}.\] Again, using \(pq=\dfrac{1}{2}\) we find \[y=2p\left(\frac{1}{2}\right)+q=p+q.\] Thus \(N\) has coordinates \((p+q,p+q)\) when \(pq=\dfrac{1}{2}\).
Show (in this case) that \(T\) and \(N\) lie on the line \(y=x\)…
When \(pq=\dfrac{1}{2}\), \(T\) has coordinates \(\left(\dfrac{1}{p+q},\dfrac{1}{p+q}\right)\), so lies on \(y=x\). And we have just shown that \(N\) has coordinates \((p+q,p+q)\), which also lies in the line \(y=x\).
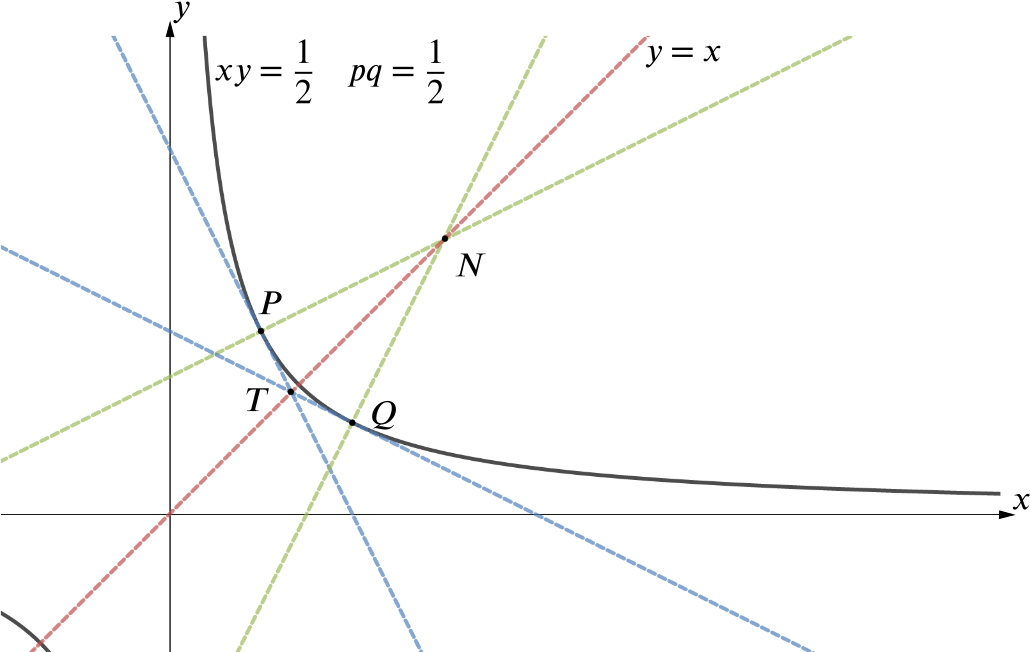
Alternatively, when \(pq = \dfrac{1}{2}\), then \(P =\left(p, \dfrac{1}{2p}\right)\) and \(Q=\left(q, \dfrac{1}{2q}\right) = \left(\dfrac{1}{2p}, p\right)\), which means by symmetry that \(T\) and \(N\) lie on \(y = x\).
…and are such that the product of their distances from the origin is constant.
We need a way to find the distance of a point from the origin. We can use Pythagoras’s theorem to do this.
The point with coordinates \((a,b)\) is at distance \(\sqrt{a^2 + b^2}\) from the origin.
The distance of \(T\) from the origin is \[\vert OT \vert = \sqrt{\frac{2}{(p+q)^2}}=\frac{\sqrt{2}}{p+q}.\] Similarly, \[\vert ON \vert = \sqrt{2(p+q)^2}=\sqrt{2}(p+q).\] Thus the product of their distances from the origin is \[\vert OT \vert \times \vert ON \vert = \frac{\sqrt{2}}{p+q} \cdot \sqrt{2}(p+q)=2,\] which is a constant.

