When does the normal to a parabola pass through this point?

Add to your resource collection Remove from your resource collection Add notes to this resource View your notes for this resource

As shown in the diagram below: \(C\) is the parabola with equation \(y=x^2\); \(P\) is the point \((0,1)\); \(Q\) is the point \((a,a^2)\) on \(C\); \(L\) is the normal to \(C\) which passes through \(Q\).

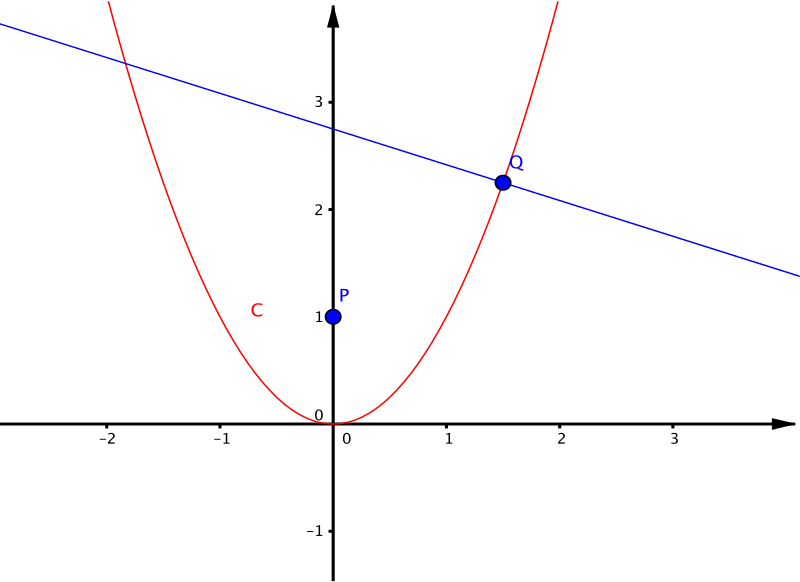
1. Find the equation of \(L\).

2. For what values of \(a\) does \(L\) pass through \(P\)?

3. Determine \(\big |QP\big |^2\) as a function of \(a\), where \(\big |QP\big |\) denotes the distance from \(P\) to \(Q\).

4. Find a point \(R\), in the \(xy\)-plane but not on \(C\), such that \(\big |RQ\big |\) is smallest for a unique value of \(a\). Briefly justify your answer.