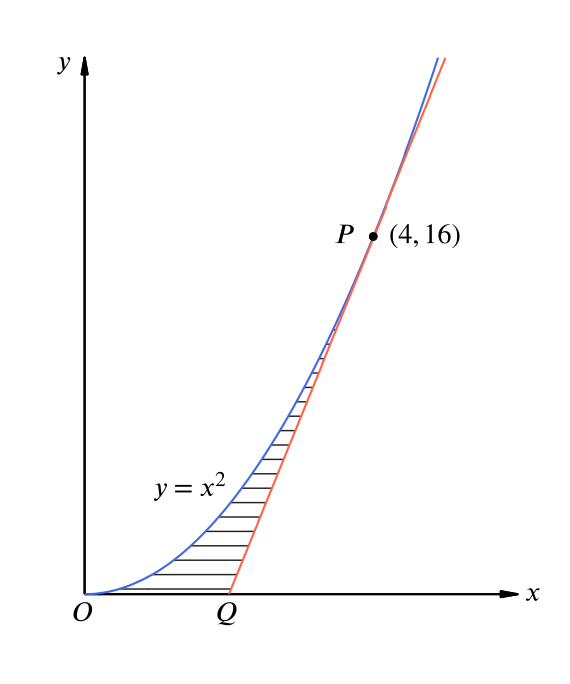
The figure shows part of the curve \(y = x^2\). \(PQ\) is the tangent to this curve at \(P\).
Calculate
- the coordinates of \(Q\),
The tangent to the curve at \(P\) intersects the \(x\)-axis at \(Q\). A sensible first step would be to calculate the equation of the tangent. This takes the form \[ y = mx + c \] where \(m\) is the gradient of the curve \(y = x^2\) at \(P\) and \(c\) is chosen so that the tangent line passes through \(P\).
The gradient of the curve \(y = x^2\) at \(P = (4,16)\) is given by \(y'=2x\) when \(x = 4\), so \(m=8\).
For the tangent line to pass through \(P\), \(c\) must be chosen so that the equation \[ 16 = 8 \times 4 + c \] is true. That is, \(c = -16\), and so the equation of the tangent is \[ y = 8x - 16. \]
The \(x\)-intercept for the tangent is the value of \(x\) for which \(y = 0\) in the equation defining the tangent.
That is, to find \(Q\) we are looking for the value of \(x\) that satisfies the equation \[ 0 = 8x - 16. \] Hence, \(x = 2\), and so \(Q = (2,0)\).
- the area of the shaded region.
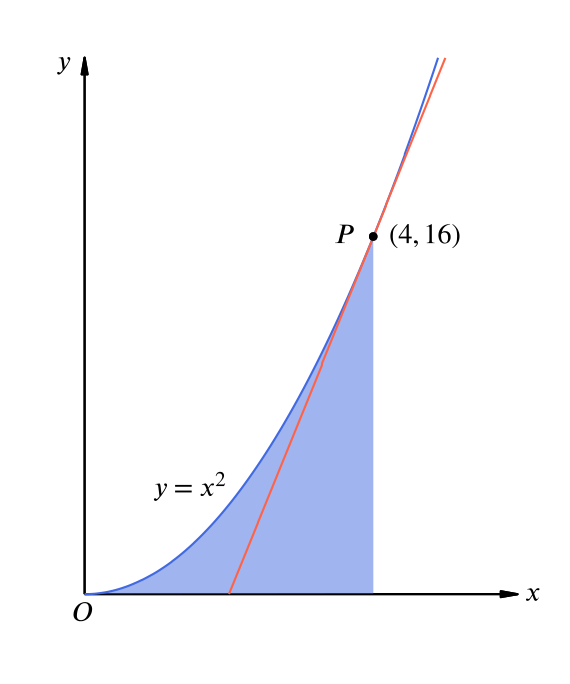
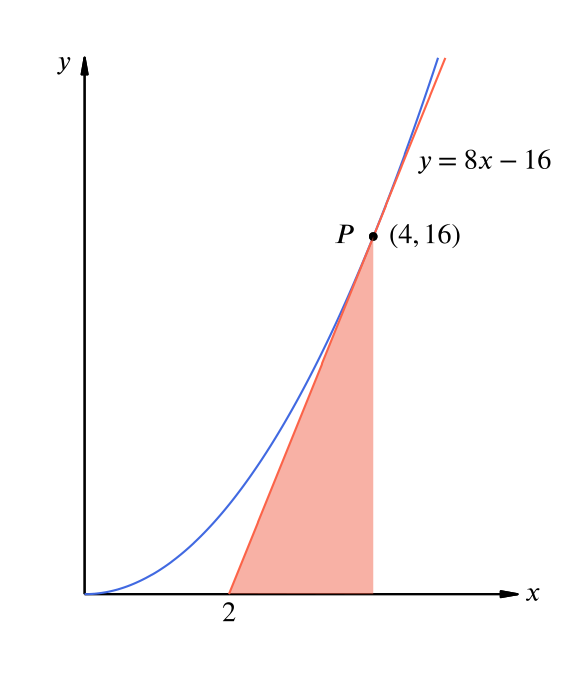
The area we are to find can be found as the area of the light blue region minus the area of the light red region.
The area of the light blue region is given by \[ \int_0^4 x^2 \:dx = \left[ \dfrac{x^3}{3} \right]_0^4 = \dfrac{4^3}{3} - \dfrac{0^3}{3} = \dfrac{64}{3}. \]
The area of the light red region is the area of a triangle, and so it equals \[ \dfrac{1}{2} \times \text{base} \times \text{height} = \dfrac{1}{2} \times (4 - 2) \times 16 = 16. \] Consequently, the desired area is \[ \dfrac{64}{3} - 16 = \dfrac{16}{3}. \]Can we generalise here? If we give the point \(P\) coordinates \((p, p^2)\), what is the required area now?

