The line \(L\) has equation \(y=c-mx\), with \(m>0\) and \(c>0\). It passes through the point \(R(a,b)\) and cuts the axes at the points \(P(p,0)\) and \(Q(0,q)\), where \(a\), \(b\), \(p\) and \(q\) are all positive. Find \(p\) and \(q\) in terms of \(a\), \(b\) and \(m\).
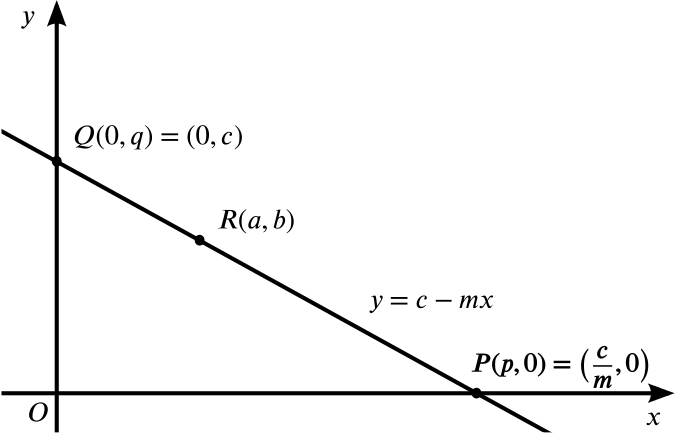
The equation of a line with gradient \(-m\), passing through the point \(R(a,b)\) is \[y-b=-m(x-a).\] We can rearrange this and compare it with the given equation for \(L\) to find that \[c= ma+b.\] Therefore we find that \(q=ma+b\) and \(p=\dfrac{ma+b}{m}\).
As \(L\) varies with \(R\) remaining fixed, show that the minimum value of the sum of the distances of \(P\) and \(Q\) from the origin is \((a^{\frac{1}{2}}+b^{\frac{1}{2}})^2\)…
Let the sum of the distances of \(P\) and \(Q\) from the origin be \(D\). Then \[D = (ma+b) + \left(\frac{ma+b}{m}\right) = ma+\frac{b}{m}+a+b.\] Since \(a\) and \(b\) are fixed, by varying \(L\) we are effectively just varying \(m\). Therefore, we want to minimise \(D\) with respect to \(m\).
Now differentiating, we have \[\frac{dD}{d m}=a-\frac{b}{m^2}.\] We get a stationary point when \(\dfrac{dD}{dm}=0\). That gives \[a=\frac{b}{m^2} \Longleftrightarrow m=\pm \sqrt{\frac{b}{a}}.\] We are told that \(m>0\), so we choose the positive root \(m=\sqrt{\frac{b}{a}}\).
This value must be a minimum value as there is only one stationary value, and by considering our expression for \(D\), we can see that as \(m\rightarrow 0, \, D\) will become very large, and the same will happen as \(m\rightarrow\infty\).
as required.
… and find in a similar form the minimum distance between \(P\) and \(Q\).
The distance \(PQ = \sqrt{p^2+q^2}\).
It’s helpful for us to note that the minimum value of \(\sqrt{p^2+q^2}\) coincides with the minimum value of \(p^2+q^2\), so we can make our lives a little easier by concentrating on minimising \[PQ^2 = p^2 + q^2 = \left(\frac{ma+b}{m}\right)^2 + (ma+b)^2\] rather than \(\sqrt{p^2+q^2}\).
Differentiating \(PQ^2\) with respect to \(m\) gives
\[\frac{d}{dm}(PQ^2) =-\frac{2ab}{m^2}-\frac{2b^2}{m^3} + 2a^2m + 2ab \]
The stationary points occur when
\[\begin{align*} -\frac{2ab}{m^2}-\frac{2b^2}{m^3} + 2a^2m + 2ab &= 0 \\ \iff \quad -\frac{b}{m^3}(am+b)+a(am+b)&=0 \\ \iff \quad \qquad (am + b)\left(a - \frac{b}{m^3}\right)&=0. \end{align*}\] The two (real) roots of this equation are \[\begin{align*} m&=-\frac{b}{a}\\ m^3&=\frac{b}{a} \quad \iff m=\sqrt[3]{\frac{b}{a}}. \end{align*}\] The first of these is not a valid root, as \(m>0\), so substituting the second back into the expression for \(PQ^2\) we find \[\begin{align*} p^2+q^2&=\left(1+\frac{1}{m^2}\right)(ma+b)^2\\ &=(1+a^{\frac{2}{3}}b^{-\frac{2}{3}})(a^{\frac{2}{3}}b^{\frac{1}{3}}+b)^2\\ &=b^{-\frac{2}{3}}(b^{\frac{2}{3}}+a^{\frac{2}{3}})(b^{\frac{1}{3}})^2(a^{\frac{2}{3}}+b^{\frac{2}{3}})^2\\ &=(a^{\frac{2}{3}}+b^{\frac{2}{3}})^3. \end{align*}\]Thus the minimum value of \(PQ= \sqrt{p^2+q^2}\) as \(L\) varies is \[(a^{\frac{2}{3}}+b^{\frac{2}{3}})^{\frac{3}{2}}.\]
As before, this value must be a minimum value as there is only one legitimate stationary value, and we can create arbitrarily large \(PQ\) by taking \(m\rightarrow 0\) or \(m\rightarrow\infty\).

