A portion of a solid sphere of radius \(a\) is cut off by means of a plane whose distance from the centre of the sphere is \(\frac{1}{2}a\). Find the volume of the portion cut off.
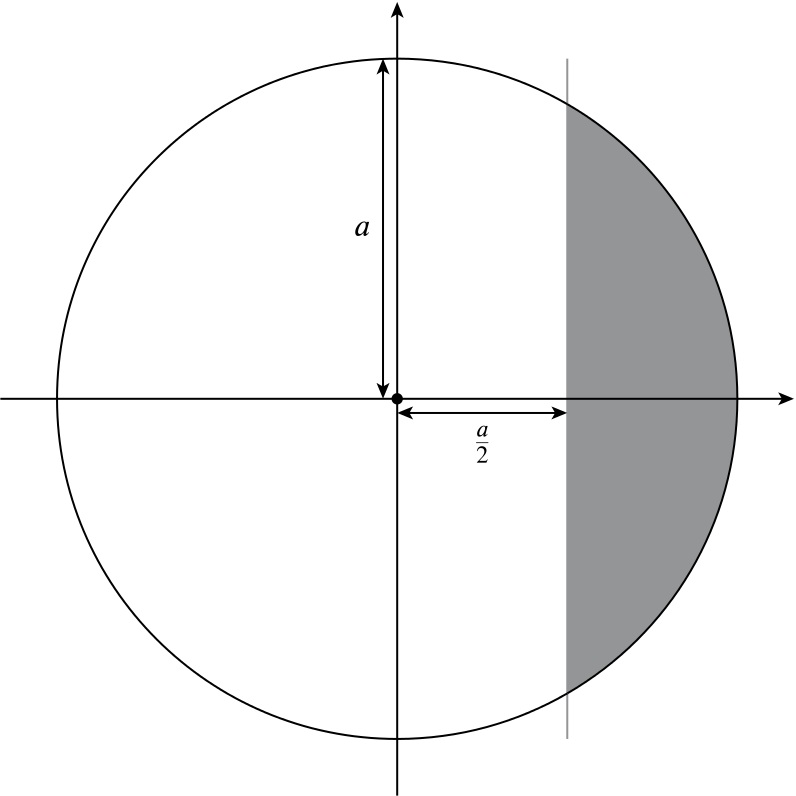
Here is a section through the centre of the sphere. With this choice of axes, the equation of the circle is \(x^2+y^2 = a^2\), and hence \(y^2=a^2-x^2\).
The portion cut off is shown in grey. Its volume can be found by revolving the circular arc for \(\frac{a}{2} < x < a\) about the \(x\)-axis.
Thus the required volume is \[\begin{align*} \int_{a/2}^a \pi y^2 \:dx &= \pi \int_{a/2}^a a^2 - x^2 \:dx \\ &= \pi \left[ a^2x - \frac{x^3}{3} \right]_{a/2}^a \\ &= \pi \left( a^3 - \frac{a^3}{3} - \frac{a^3}{2} + \frac{a^3}{24} \right) \\ &= \pi a^3 \left( \frac{24 - 8 - 12 + 1}{24} \right ) \\ &= \frac{5}{24} \pi a^3. \end{align*}\]Find also the distance from the circular plane face of the centre of gravity of this portion.
By symmetry, the centre of gravity (or centre of mass) lies on the \(x\)-axis in our diagram. To find out where on the axis, we take moments about \(O\) and treat the sphere as having density of \(1\).
We divide the grey solid into discs, each with its centre \(x\) from \(O\), with thickness \(\delta x\) and radius \(y\). The volume of a disc is \(\pi y^2 \delta x\).
The moment of each disc about \(O\) is \(x \pi y^2 \delta x\).
We now let the thickness of the discs tend to zero, at which point the sum of these moments becomes an integral. Let the centre of mass of the grey portion be at a distance \(\bar x\) from \(O\).
\[\begin{align*} \bar x \frac{5}{24} \pi a^3 &= \int_{a/2}^a x \pi y^2 \:dx\\ &= \pi\int_{a/2}^a x(a^2 - x^2) \:dx \\ &= \pi\left[ \frac{a^2x^2}{2} - \frac{x^4}{4} \right]_{a/2}^a\\ &= \pi\left( \frac{a^4}{2} - \frac{a^4}{4} - \frac{a^4}{8} + \frac{a^4}{64} \right) \\ &= \pi\frac{9}{64} a^4, \end{align*}\] and therefore \[\begin{equation*} \bar x = \frac{\frac{9}{64} \pi a^4}{\frac{5}{24} \pi a^3} = \frac{27}{40} a. \end{equation*}\] The required distance from the plane is therefore \[\begin{equation*} \frac{27}{40} a - \frac{1}{2} a = \frac{7}{40} a. \end{equation*}\]It is interesting to note that the centre of mass is not the same as the point which has exactly half the mass of the grey solid on each side of it. This latter point, \(\bar X\), can be found by integration and is such that \(\bar X \approx 0.6571 a\), whereas the centre of mass, \(\bar x = 0.675 a\).
This is equivalent to the distinction between the median and the mean of the distribution of mass.

