Let \(P\) be the point on the curve \(y=ax^2+bx+c\) (where \(a\) is non-zero) at which the gradient is \(m\). Show that the equation of the tangent at \(P\) is \[y-mx=c-\frac{(m-b)^2}{4a}.\]
The gradient of the quadratic is \[\frac{dy}{dx}=2ax+b=m.\]
Let the coordinates at \(P\) be \(P(x_P,y_P)\). Then \[\begin{align*} x_P &= \frac{m-b}{2a}, \quad \textrm{and} \\ y_P &= a\left(\frac{m-b}{2a}\right)^2+b\left(\frac{m-b}{2a}\right)+c. \end{align*}\] Thus the tangent at \(P\) has the equation \[y-\left[a\left(\frac{m-b}{2a}\right)^2+b\left(\frac{m-b}{2a}\right)+c\right] = m\left(x-\frac{m-b}{2a}\right),\] that is, \[\begin{align*} y-mx &= \frac{(m-b)^2}{4a}+\frac{b(m-b)}{2a}+c-\frac{m(m-b)}{2a}\\ &= c+\frac{1}{4a}(m-b)\left[2b-2m+(m-b)\right]\\ &= c- \frac{(m-b)^2}{4a} \end{align*}\]as required.
Show that the curves \(y=a_1x^2+b_1x+c_1\) and \(y=a_2x^2+b_2x+c_2\) (where \(a_1\) and \(a_2\) are non-zero) have a common tangent with gradient \(m\) if and only if \[(a_2-a_1)m^2+2(a_1b_2-a_2b_1)m+4a_1a_2(c_2-c_1)+a_2b_1^2-a_1b_2^2=0.\]
as required.
Show that, in the case \(a_1\neq a_2\), the two curves have exactly one common tangent if and only if they touch each other.
If \(a_1\neq a_2\) then to get exactly one root of \(\eqref{eq:1}\) we need the discriminant of the quadratic to be zero, that is, \[4(a_1b_2-a_2b_1)^2=4(a_2-a_1)(4a_1a_2(c_2-c_1)+a_2b_1^2-a_1b_2^2),\] so \[-2a_1a_2b_1b_2=4a_1a_2(a_2-a_1)(c_2-c_1)-a_1a_2b_1^2-a_1a_2b_2^2.\] Since \(a_1\) and \(a_2\) are non-zero by definition, we can cancel the \(a_1a_2\) factor: \[b_1^2-2b_1b_2+b_2^2=4(a_1-a_2)(c_2-c_1),\] so \[(b_2-b_1)^2=4(a_2-a_1)(c_2-c_1).\] The curves touch if and only if there is exactly one solution to \[a_1x^2+b_1x+c_1=a_2x^2+b_2x+c_2,\] that is, \[(a_2-a_1)x^2+(b_2-b_1)x+(c_2-c_1)=0.\] For one solution we need \[(b_2-b_1)^2=4(a_2-a_1)(c_2-c_1)\] which is the same condition for having exactly one common tangent.
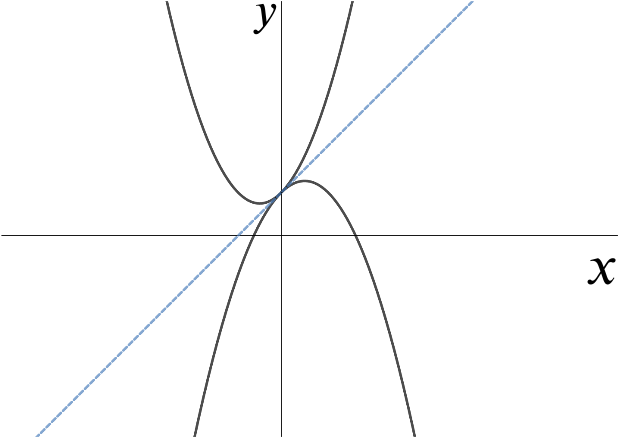
In the case \(a_1=a_2\), find a necessary and sufficient condition for the two curves to have exactly one common tangent.
If \(a_1=a_2\) then there is exactly one solution to \[2a_1(b_2-b_1)m+4a_1^2(c_2-c_1)+a_1(b_1^2 - b_2^2)=0.\] This is a linear equation and the only condition needed for there to be a solution for \(m\) is \(b_1\neq b_2\).
If \(b_1 = b_2\), then there are no solutions for \(m\) unless \(c_1 = c_2\), in which case there are infinitely many solutions.

