A cuboid has a total surface area of \(\quantity{150} {cm^2}\) and is such that its base is a square of side \(\quantity{x}{cm}\).
Show that the height, \(\quantity{h}{cm}\), of the cuboid is given by \(h=\frac{75-x^2}{2x}\).
A cuboid with side lengths \(x\), \(x\) and \(h\) has a surface area of\[S=2x^2+4xh.\]
We know that the total surface area should be \(\quantity{150} {cm^2}\), so
\[\begin{align*} 150 &= 2x^2+4xh\\ \implies 150 -2x^2 &= 4xh\\ \implies h &= \frac{75-x^2}{2x}. \end{align*}\]Express the volume of the cuboid in terms of \(x\).
A cuboid with side lengths \(x\), \(x\) and \(h\) has a volume of \(V=x^2h\). Now
\[\begin{align*} V &= x^2h\\ &= x^2\bigl(\frac{75-x^2}{2x}\bigr)\\ &= \frac{75}{2}x-\frac{1}{2}x^3. \end{align*}\]Hence determine, as \(x\) varies, its maximum volume and show that this volume is a maximum.
We have \(V\) as a function of \(x\), so to find the stationary points we differentiate, and set the result equal to zero. We have
\[V' (x) = \frac{75}{2} - \frac{3}{2} x^2.\]
Putting this equal to zero, we see
\[\begin{align*} \frac{75}{2} - \frac{3}{2} x^2 &=0\\ \implies \frac{75}{2} &= \frac{3}{2} x^2 \\ \implies 25 &= x^2 \\ \implies x &= \pm5. \end{align*}\]Since \(x\) is a length, it must be positive, implying \(x=5\).
Is our solution a maximum? We know \(V = 0.5x(75-x^2)\), and so the equation \(V=0\) has three roots, \(0\) and \(\pm \sqrt{75}\). Given the coefficient of \(x^3\) is negative, the curve must look like this:
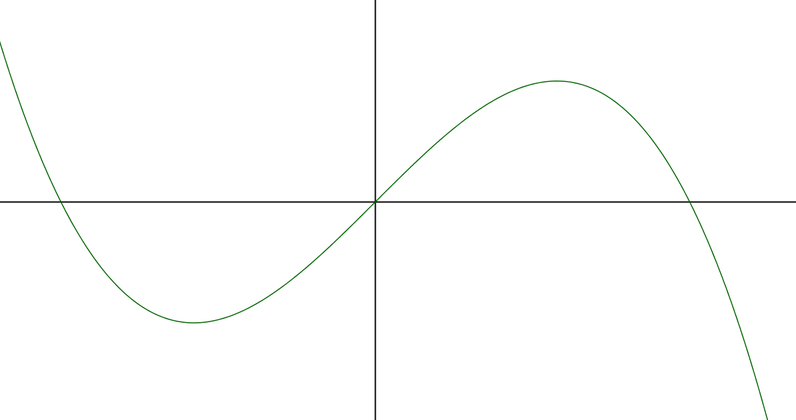
Thus \(x = 5\) gives us a maximum for \(V\).
Or we could show \(x = 5\) gives a maximum by evaluating the second derivative of \(V\), giving
\[\begin{align*} V''(x)&=-3x\\ \implies V''(5) &=-15. \end{align*}\]The second derivative is negative at \(x=5\), so the volume has a maximum here, as required.
Now all that remains is to find the volume of the cuboid when \(x=5\), which is given by
\[\begin{align*} V(x) &= \frac{75}{2}x-\frac{1}{2}x^3 \\ \implies V(5) &= \frac{75}{2} \times 5 - \frac{1}{2} \times 5^3 \\ &= \frac{375}{2} - \frac{125}{2} \\ &= \frac{250}{2} \\ &= 125. \end{align*}\]Therefore the maximum volume of the cuboid is \(\quantity{125} {cm^3}\).

